Дифференциальный редуктор — Википедия
Материал из Википедии — свободной энциклопедии
(перенаправлено с «»)Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 мая 2015; проверки требуют 23 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 мая 2015; проверки требуют 23 правки.
 Планетарный редуктор.
Планетарный редуктор.Опорное звено эпицикл заблокировано на корпус редуктора.
Планета́рный реду́ктор, дифференциа́льный реду́ктор (от лат. differentia – разность, различие) — один из классов механических редукторов. Редуктор называется планетарным из-за планетарной передачи, находящейся в редукторе, передающей и преобразующей крутящий момент.
Общее описание[ | ]

Конструкция[ | ]
Механической основой планетарного редуктор может быть планетарная передача любой формы и состава. Принципиальная возможность работы планетарной передачи в режиме редуктора не зависит от формата распределения функций между тремя её основными звеньями (солнцем, водилом и эпициклом): любое звено может быть выбрано конструкторами как ведущее, и любое как ведомое. Но при этом, наличие у планетарной передачи двух степеней свобод требует снятия одной степени свободы для её работы в качестве редуктора; эта задача решается посредством блокировки третьего звена на корпус редуктора, а само звено получает название «
Уникальные особенности[ | ]
В контексте сравнения планетарной передачи с любыми другими типами зубчатых передач под использование их в качестве редуктора, таковыми особенностями являются: соосность входящего и исходящего потока мощности (например, валов) даже на однорядной планетарной передаче; возможность выбора из шести передаточных отношений даже на простой трёхзвенной планетарной передаче; две степени свободы любой планетарной передачи; возможность получения больших передаточных отношений в условиях ограниченного поперечного габарита.
Типы планетарных редукторов и их применение[ | ]
Шуруповёрт в разобранном виде. Справа видны сателлиты и эпицикл первой скорости редуктора.Дифференциальный редуктор Википедия

Опорное звено эпицикл заблокировано на корпус редуктора.
Планета́рный реду́ктор, дифференциа́льный реду́ктор (от лат. differentia – разность, различие) — один из классов механических редукторов. Редуктор называется планетарным из-за планетарной передачи, находящейся в редукторе, передающей и преобразующей крутящий момент.
Общее описание[ | ]

Конструкция[ | ]
Механической основой планетарного редуктора может быть планетарная передача любой формы и состава. Принципиальная возможность работы планетарной передачи в режиме редуктора не зависит от формата распределения функций между тремя её основными звеньями (солнечной шестернёй, водилом с шестернями сателлитами и коронной шестернёй): любое звено может быть выбрано конструкторами как ведущее, и любое как ведомое. Но при этом, наличие у планетарной передачи двух степеней свобод требует снятия одной степени свободы для её работы в качестве редуктора; эта задача решается посредством блокировки третьего звена на корпус редуктора, а само звено получает название «
Уникальные особенности[ | ]
В контексте сравнения планетарной передачи с любыми другими типами зубчатых передач под использование их в качестве редуктора, таковыми особенностями являются: соосность входящего и исходящего потока мощности (например, валов) даже на однорядной планетарной передаче; возможность выбора из шести передаточных отношений даже на простой трёхзвенной планетарной передаче; две степени свободы любой планетарной передачи; возможность получения больших передаточных отношений в условиях ограниченного поперечного габарита.
Типы планетарных редукторов и их применение
Планетарная передача — Википедия

 Планетарная передача (солнечная шестерня остановлена)
Планетарная передача (солнечная шестерня остановлена)  Планетарная передача (коронная шестерня остановлена)
Схема эпициклически движущейся планеты
Планетарная передача (коронная шестерня остановлена)
Схема эпициклически движущейся планетыПланетарная передача (далее — ПП
Конструктивно ПП всегда представляет собой набор взаимозацепленных зубчатых колёс (не менее 4), часть из которых (не менее 2) имеет общую геометрическую неподвижную ось вращения, а другая часть (также, не менее 2) имеет подвижные оси вращения, концентрически вращающиеся на так называемом «водиле» вокруг неподвижной. Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую, а через зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться относительно первых, но и обкатывать их, тем самым передавая поступательное движение на водило, все звенья ПП, на которые можно подавать/снимать мощность, получают возможность вращаться дифференциально, с тем лишь условием, что угловая скорость любого такого звена не абсолютно хаотична, а определяется угловыми скоростями всех остальных звеньев. В этом плане ПП похожа на планетарную систему, в которой скорость каждой планеты определяется скоростями всех остальных планет системы. Дифференциальный принцип вращения всей системы, а также то, что в своём каноническом виде набор зубчатых колёс, составляющих ПП, собран в некоем подобии солнца и эпициклически движущихся по орбите планет, даёт данной механической передаче такие присущие только ей интернациональные определения, как
С точки зрения теоретической механики планетарная передача — это механическая система с двумя и более степенями свободы. Эта особенность, являющаяся прямым следствием конструкции, есть важное отличие ПП от каких-либо других передач вращательного движения, всегда имеющих только одну степень свободы. И эта особенность наделяет саму ПП тем важным качеством, что в аспекте воздействия на угловые скорости вращения ПП может не только редуцировать эти скорости, но и складывать и раскладывать их, что, в свою очередь, делает её основным механическим исполнительным узлом не только различных планетарных редукторов, но таких устройств, как дифференциалы и суммирующие ПП.
Планетарная передача и планетарный механизм[править | править код]
В русскоязычной инженерной терминологии термины планетарная передача (далее — ПП) и планетарный механизм (далее — ПМ) зачастую предполагаются как синонимы. Отличия в том, что термин ПП обычно используется в контексте принципиального понимания устройства той или иной передачи вращательного движения, особенно если устройство такой передачи не очевидно (скрыто корпусом/картером) или такая передача обладает определёнными уникальными свойствами, присущими только планетарной, и на этом надо акцентировать внимание. А термин ПМ используется для обозначения конкретного зубчато-рычажного механизма, причём существуют критерии, позволяющие чётко описать ПМ как сборочный узел в составе более крупного узла или агрегата и определить, сколько и каких именно использовано ПМ в конкретной передаче вращательного движения.
Состав планетарного механизма[править | править код]
Конструкция ПП/ПМ основана на различных комбинациях из трёх основных и нескольких одинаковых вспомогательных звеньев. Три основные звена с одной общей осью вращения — два центральных зубчатых колеса и водило. Вспомогательные звенья — набор одинаковых зубчатых колёс на подвижных осях вращения и подшипники.
- Большое центральное зубчатое колесо с внутренними зубьями называется коронной, эпициклической шестернёй или эпициклом (Э).
- Водило (В) является основой ПМ — это неотъемлемая деталь абсолютно любого ПМ и краеугольный камень всей идеи передачи вращения через планетарную систему с дифференциальной связью. Водило представляет собой рычажный механизм — обычно такую пространственную вилку, ось «основания» которой совпадает с осью самого ПМ, а оси «зубцов» с установленными на них сателлитами концентрически вращаются вокруг неё в плоскости/плоскостях расположения центральных зубчатых колёс. Оси «зубцов» — это и есть так называемые подвижные оси или оси сателлитов
- Сателлиты () представляют собой зубчатые колёса (или группы колёс) с внешними зубьями. При этом сателлиты находятся в одновременном и постоянном зацеплении с обоими центральными зубчатыми колёсами ПМ. Количество сателлитов в ПМ обычно составляет от двух до шести (чаще всего — три, так как только при трёх сателлитах нет нужды в специальных уравновешивающих механизмах) и точного значения для функциональности ПМ не имеет. В различных ПМ применяются сателлиты одновенцовые (одно простое зубчатое колесо), двухвенцовые (два соосных зубчатых колеса с общей ступицей), трёхвенцовые и так далее. Также сателлиты могут быть парными — то есть, располагающимимся на осях одного водила и зацепленными в паре.
Зубчатые колёса, составляющие ПМ, могут быть любого известного типа: прямозубые, косозубые, шевронные, червячные. Тип зацепления в общем случае не важен и на принципиальную работу ПП влияния не оказывает.
В любом ПМ оси вращения центральных зубчатых колёс и водила всегда совпадают. Однако это не значит, что оси сателлитов всегда будут параллельны основной оси. Как и в случае с простыми зубчатыми передачами, здесь возможны варианты параллельных, скрещивающихся и пересекающихся осей. Пример второго варианта — межколёсный дифференциал с коническими зубчатыми колёсами. Пример третьего варианта — самоблокирующийся дифференциал Torsen с червячным зацеплением.
Любой ПМ, независимо простой он или сложный, плоский или пространственный, для своей работоспособности должен иметь одно водило с сателлитами и не менее двух любых центральных зубчатых колёс. Под определением «два любые» подразумевается, что это могут быть не только одно солнце и один эпицикл, но и два солнца и ни одного эпицикла, или два эпицикла и ни одного солнца. Три звена, в том числе водило, есть необходимое и достаточное условие для того, чтобы ПМ мог выполнять функции передачи мощности и сложения/разложения потоков: работать в качестве редуктора (в том числе многоскоростного), в качестве дифференциала или суммирующей ПП. Также три звена есть основа такого русскоязычного технического термина, как Трёхзвенный Дифференциальный Механизм (или ТДМ).
Формально, механизмы, состоящие всего из двух звеньев — из водила и всего лишь одного центрального зубчатого колеса — также могут именоваться планетарными. Фактически же, такие двухзвенные ПМ трудно разумно приспособить для выполнения какой-либо работы: они не годятся для передачи мощности с одного основного звена на другое и лишь при определённых условиях могут работать как переусложнённая прямая передача. Увеличение числа основных звеньев одного ПМ в большую сторону — до 4 и более — возможно и формально и фактически, однако при этом такие ПМ не приобретают никаких новых свойств, хотя и получают больше теоретически доступных передаточных отношений и могут давать проектируемой ПП определённые компоновочные преимущества.
Простые и сложные ПМ, планетарный ряд[править | править код]
Схемы наиболее распространённых сложных планетарных механизмовКритерием деления ПМ на простые и сложные является число составляющих его основных звеньев (именно основных, а число сателлитов — не в счёт). Простой ПМ имеет всего три основных звена: одно водило и два любых центральных зубчатых колеса. Кинематика допускает всего-лишь 7 (семь!) ПМ, подпадающих под это условие: один наиболее распространённый и всем известный, так называемый «элементарный», с набором одновенцовых сателлитов схемы ; три ПМ с двухвенцовыми саттелитами (, , ) и три ПМ с парными взаимозацепленными сателлитами (СВЭ, СВС, ЭВЭ)).
Сложных ПМ гораздо больше чем простых. Их точное число не определено ввиду отсутствия такой нужды, а наиболее распространённые из них приведены на рисунке. Точно так же как и простые ПМ, сложные имеют всего одно водило, но центральных зубчатых колёс может быть три и более. При этом в составе сложного ПМ всегда умозрительно можно выделить несколько простых ПМ (конкретно: три в четырёхзвенном и шесть в пятизвенном), каждый из которых в себя включает два каких-то центральных зубчатых колеса и одно общее водило.
Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой ПМ с набором одновенцовых сателлитов является однорядным. Все три простые ПМ с двухвенцовыми сателлитами — двухрядные. ПМ с парными взаимозацепленными сателлитами схемы СВЭ — однорядный; схем СВС и ЭВЭ — двухрядные. Таким образом, все простые ПМ могут быть или однорядными или двухрядными. Сложные ПМ, в свою очередь, могут быть двух, трёх и четырёхрядные. Верхнее число рядов в сложном ПМ формально не ограничено, хотя фактически уже пятирядные есть большая редкость, хотя в сборках из планетарных механизмов, применяющихся в многоступенчатых планетарных коробках передач, общее число рядов может быть пять и больше. Нередко термины ПМ и планетарный ряд предполагаются как синонимы, но, в общем случае, это неверно: даже если в отдельных случаях оба термина могут обозначать одно и то же, всегда следует помнить, что их смыл несколько разный.
Плоские и пространственные ПМ[править | править код]
Свободный дифференциал на основе простого плоского двухрядного ПМ с парными сателлитами Свободный дифференциал на основе пространственного ПМ с коническими шестернямиНаличие в составе одного ПМ более одного планетарного ряда не означает, что он является пространственным. Сколько бы ни было рядов, но если плоскости вращения всех составляющих каждый ряд зубчатых колёс параллельны, то такой ПМ будет оставаться плоским. Критерием отличия плоского ПМ от пространственного является наличие не просто более одной плоскости вращения составляющих его зубчатых колёс, но наличие непараллельных плоскостей их вращения. Плоскости вращения звеньев в пространственном ПМ не обязаны быть строго перпендикулярны друг-другу и могут находиться под любыми произвольными углами. Примером пространственного ПМ может служить конический симметричный дифференциал, наподобие применяющегося в приводе ведущих колёс автомобиля. А вот близкий по конструкции цилиндрический дифференциал, применяющийся там же и выполняющий точно такие же функции, будет оставаться плоским ПМ.
Пространственные ПМ по своему функционалу ничем не отличаются от аналогичных по составу плоских ПМ. Выбор того или иного ПМ в качестве основы конкретной ПП есть лишь вопрос экономики или конструкторских предпочтений. Тот же простой межколёсный дифференциал почти всегда выполнен на основе пространственного ПМ не потому, что что плоский не годится, а, скорее, по определённым компоновочным соображениям. Плюс, как это ни странно, пространственный ПМ для выполнения схожих функций может требовать меньшего количества шестерён и деталей вообще. Так, тот же межколёсный дифференциал в пространственном варианте требует всего лишь 4 одинаковые шестерни, из которых две пойдут на два солнца и две — на два саттелита. В случае же плоского варианта, таких шестерён потребуется как минимум шесть, а скорее всего — восемь, и при этом они обязательно будут двух разных типоразмеров.
2 степени свободы ПМ[править | править код]
Уникальной особенностью любого ПМ, отличающей его от всех прочих зубчатых передач, является наличие у него двух степеней свободы. Применительно к простому трёхзвенному ПМ это означает, что понимание угловой скорости вращения любого одного основного звена не даёт однозначного понимания угловых скоростей двух других основных звеньев, даже если известны все передаточные отношения внутри ПМ. Здесь все три основных звена находятся в дифференциальной связи друг с другом и для определения их угловых скоростей надо знать угловые скорости как минимум двух из них. В этом есть важное отличие ПМ от прочих зубчатых механизмов, в которых угловые скорости всех элементов связаны линейной зависимостью, а по угловой скорости одного элемента всегда можно точно определить угловые скорости всех остальных элементов, сколь много их бы не было. И в этом есть основа уникальных свойств, присущих любому ПМ: способность изменять угловые скорости на выходе при неизменных угловых скоростях на входе, способность делить и суммировать потоки мощности и всё это при постоянно зацепленных шестернях.
Любой ПМ, независимо от того, простой он или сложный, имеет фактически лишь две степени свободы. Для простого ПМ это подтверждается и визуальным наблюдением за работой такого механизма и уравнением Чёбышева. Для сложных ПМ это визуально не очевидно, а уравнение Чёбышева теоретически может допускать существование для таких ПМ трёх степеней свобод, что подразумевает наличие четырёх звеньев, находящихся в дифференциальной связи друг с другом. Но фактически такие сложные ПМ будут физически неработоспособны в тех практических задачах, ради которых они создаются, а все работоспособные сложные ПМ останутся двухстепенными. Независимо от числа основных звеньев любого работоспособного сложного ПМ, в нём, так же как и в простом ПМ, в дифференциальной связи друг с другом будет находиться только три основных звена, а остальные основные звенья, сколько бы их ни было, будут иметь линейную связь с каким-то одним из трёх вышеупомянутых. Попытки же создания сложных ПМ с тремя (и тем более, с четырьмя) фактическими степенями свободы считаются бесперспективными, а все работоспособные трёх- и четырёхстепенные ПП основаны на сборке последовательно взаимозацепленных двухстепенных ПМ.
Передаточное отношение[править | править код]
 Планетарная передача в режиме повышения скорости. Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.
Планетарная передача в режиме повышения скорости. Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение различными способами.
При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, а два других служат в качестве ведущего и ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также от того, какой элемент закреплён.
Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как S{\displaystyle S}, а для планетарных шестерён примем это число как P{\displaystyle P}, то передаточное отношение будет определяться формулой SP{\displaystyle {\frac {S}{P}}}, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет −2416{\displaystyle -{\frac {24}{16}}}, или −32{\displaystyle -{\frac {3}{2}}}, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.
Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет A{\displaystyle A} зубьев, то оно будет вращаться с соотношением PA{\displaystyle {\frac {P}{A}}} относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 1664{\displaystyle {\frac {16}{64}}}, или 14{\displaystyle {\frac {1}{4}}}. Таким образом, объединив оба примера, мы получим следующее:
- Один оборот солнечной шестерни даёт −SP{\displaystyle -{\frac {S}{P}}} оборотов планетарных шестерён;
- Один оборот планетарной шестерни даёт PA{\displaystyle {\frac {P}{A}}} оборотов кольцевой.
В итоге, если водило заблокировано, общее передаточное отношение системы будет равно −SA{\displaystyle -{\frac {S}{A}}}.
В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет меньше единицы и составит 1(1+AS){\displaystyle {\frac {1}{(1+{\frac {A}{S}})}}}.
Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно 1+AS{\displaystyle 1+{\frac {A}{S}}}. Это самое большое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.
Всё вышесказанное можно описать следующими двумя уравнениями (выведены из условия отсутствия проскальзывания сопрягаемых шестерён и следовательно равенства дуг, проходимых точками, находящихся на окружностях, в единицу времени):
- A(ωa−ωc)=PωpS(ωs−ωc)=−Pωp{\displaystyle {\begin{aligned}A\left(\omega _{a}-\omega _{c}\right)=P\omega _{p}\\S\left(\omega _{s}-\omega _{c}\right)=-P\omega _{p}\end{aligned}}}
Здесь ωa,ωc,ωp,ωs{\displaystyle \omega _{a},\omega _{c},\omega _{p},\omega _{s}} — угловые скорости соответственно: кольцевой шестерни, водила, планетарных шестерён относительно водила, и солнечной шестерни. Первое уравнение характеризует вращение водила относительно кольцевой шестерни, второе — солнечной шестерни относительно водила.
Если исключить из уравнений ωp{\displaystyle \omega _{p}} путём их сложения — получится одно уравнение: Aωa+Sωs=(A+S)ωc{\displaystyle A\omega _{a}+S\omega _{s}=(A+S)\omega _{c}}. Так как числа зубьев шестерён всегда удовлетворяют условию A=S+2P{\displaystyle A=S+2P} (исходя из простых геометрических соотношений, поскольку в диаметр коронной шестерни помещается диаметр солнечной шестерни и два диаметра сателлитов), по-другому это уравнение можно записать как:
(2+n)ωa+nωs−2(1+n)ωc=0{\displaystyle \left(2+n\right)\omega _{a}+n\omega _{s}-2\left(1+n\right)\omega _{c}=0}
Где n — это параметр передачи, равный n=SP{\displaystyle n={S \over P}}, то есть отношению чисел зубьев солнечной и планетарных шестерён.
В нижеуказанной таблице (указывающей выходные скорости различных типов планетарных передач в зависимости от их конструктивных особенностей) приняты следующие условные обозначения:
Дифференциальный редуктор Вики
Планетарный редуктор.Опорное звено эпицикл заблокировано на корпус редуктора.
Планета́рный реду́ктор, дифференциа́льный реду́ктор (от лат. differentia – разность, различие) — один из классов механических редукторов. Редуктор называется планетарным из-за планетарной передачи, находящейся в редукторе, передающей и преобразующей крутящий момент.
Общее описание[ | код]
Колёсный редуктор военного автомобиля МАЗ-7310. Водило с сателлитами снятыКонструкция[ | код]
Механической основой планетарного редуктора может быть планетарная передача любой формы и состава. Принципиальная возможность работы планетарной передачи в режиме редуктора не зависит от формата распределения функций между тремя её основными звеньями (солнечной шестернёй, водилом с шестернями сателлитами и коронной шестернёй): любое звено может быть выбрано конструкторами как ведущее, и любое как ведомое. Но при этом, наличие у планетарной передачи двух степеней свобод требует снятия одной степени свободы для её работы в качестве редуктора; эта задача решается посредством блокировки третьего звена на корпус редуктора, а само звено получает название «опорное звено».
Уникальные особенности[ | код]
В контексте сравнения планетарной передачи с любыми другими типами зубчатых передач под использование их в качестве редуктора, таковыми особенностями являются: соосность входящего и исходящего потока мощности (например, валов) даже на однорядной планетарной передаче; возможность выбора из шести передаточных отношений даже на простой трёхзвенной планетарной передаче; две степени свободы любой планетарной передачи; возможность получения больших передаточных отношений в условиях ограниченного поперечного габарита.
Типы планетарных редукторов и их применение[ | код]
Планетарный редуктор с одной степенью свободы[ | код]
В таких редукторах опорное звено всегда заблокировано на корпус редуктора. При этом для любой трёхзвенной планетарной передачи возможны шесть вариантов распределения ролей между тремя основными звеньями, что даёт шесть передаточных отношений, три из которых могут применяться для редукторов (передаточное отношение больше единицы) и три для мультипликаторов (передаточное отношение меньше единицы).
Наиболее глубокую редукцию в схеме СВЭ даёт вариант 1 (с солнечной шестерни на водило), наиболее слабую — вариант 3 (с коронной шестерни на водило). Некое промежуточное значение редукции с обязательным противовращением даёт Вариант 5 (с солнечной шестерни на коронную), но в силу разных причин его используют не часто (единственный известный пример — колёсные редукторы дорожных автомобилей МАЗ). Оставшиеся три варианта дают мультипликацию, в том числе одно передаточное отношение обратного вращения.
Планетарные редукторы с одной степенью свободы применяются в бортовых главных передачах гусеничных машин, в двухступенчатых главных передачах колёсных грузовых машин в ступицах ведущих колёс, в грузовых лебёдках и тельферах, в автомобильных стартёрах, в совмещённых планетарных мотор-редукторах. Общий принцип применения — требование компактности редуктора и соосности ведущего и ведомого валов. В грузовых лебёдках и тельферах могут применяться двух- и трёхрядные планетарные передачи, а общее передаточное отношение таких планетарных редукторов может быть порядка 100.
Планетарный редуктор с двумя степенями свободы[ | код]
Конструктивно подобный планетарный редуктор может быть аналогичен планетарному редуктору с одной степенью свободы, с тем лишь отличием, что опорное звено здесь может быть разблокировано. При этом планетарная передача перестаёт выполнять редукцию и становится дифференциалом, а ввиду того, что в любом дифференциале мощность на ведомых звеньях выравнивается до минимально востребованной на любом из двух этих звеньев, настоящее ведомое звено перестаёт передавать сколь-либо существенную мощность по кинематической цепи трансмиссии и останавливается, а вращается только разблокированное опорное звено. К подобным редукторам относится термин «дифференциальный редуктор».
Применяются в однорадиусных механизмах поворота гусеничных машин, где они одновременно выполняют функцию редукции и обеспечивают возможность плавного разрыва потока мощности. Также могут применяться везде, где требуется опция отключения потока мощности без необходимости остановки мотора или вала привода ведущего звена.
Многоскоростной планетарный редуктор[ | код]
Многоскоростные планетарные редукторы допускают переключение между различными кинематическими цепями внутри себя, то есть, дают возможность использования разных передаточных отношений. Конструктивно это всегда реализуется через применение так называемых управляющих элементов: тормозов, блокировочных фрикционов, обгонных муфт. Наличие шести передаточных отношений даже на одном простом планетарном механизме теоретически допускает его использование в качестве минимально возможного, но фактически все многоскоростные планетарные редукторы выполнены либо на основе одного сложного планетарного механизма, либо на основе нескольких последовательно зацепленных простых (и сложных) планетарных механизмов. Число степеней свободы таких редукторов может быть 2 и более, общее число управляющих элементов может быть более десяти. Все многоскоростные планетарные редукторы имеют ту особенность, что взаимная блокировка их звеньев превращает их в прямую передачу, что может быть также использовано для расширения числа доступных скоростей.
В основном применяются в трансмиссиях транспортных машин: в двухрадиусных механизмах поворота гусеничных машин, в коробках передач и раздаточных коробках колёсных и гусеничных машин, где могут выполнять как функции делителя, овердрайва, ходоуменьшителя, так и функции основного набора передач включая реверс, независимо от общего числа скоростей. Также применяются в электроинструментах, где требуется возможность получения более одной скорости вращения.
Шарикоподшипниковый редуктор[ | код]
Шарикоподшипник представляет пример планетарного редуктора, в котором водилом является сепаратор, функции солнечной шестерни выполняет внутреннее кольцо, функции коронной шестерни — наружное кольцо, а сателлиты — это шарики. С использованием обыкновенных шарикоподшипников могут быть сконструированы маломощные редукторы (для научных или измерительных приборов). Например, шарикоподшипниковые планетарные редукторы используются в конструкции верньера, применяемого для точной настройки радиостанции на нужную частоту приема/передачи.
См. также[ | код]
Примечания[ | код]
Ссылки[ | код]
Дифференциальный редуктор Википедия
Планетарный редуктор.Опорное звено эпицикл заблокировано на корпус редуктора.
Планета́рный реду́ктор, дифференциа́льный реду́ктор (от лат. differentia – разность, различие) — один из классов механических редукторов. Редуктор называется планетарным из-за планетарной передачи, находящейся в редукторе, передающей и преобразующей крутящий момент.
Общее описание
Колёсный редуктор военного автомобиля МАЗ-7310. Водило с сателлитами снятыКонструкция
Механической основой планетарного редуктора может быть планетарная передача любой формы и состава. Принципиальная возможность работы планетарной передачи в режиме редуктора не зависит от формата распределения функций между тремя её основными звеньями (солнечной шестернёй, водилом с шестернями сателлитами и коронной шестернёй): любое звено может быть выбрано конструкторами как ведущее, и любое как ведомое. Но при этом, наличие у планетарной передачи двух степеней свобод требует снятия одной степени свободы для её работы в качестве редуктора; эта задача решается посредством блокировки третьего звена на корпус редуктора, а само звено получает название «опорное звено».
Уникальные особенности
В контексте сравнения планетарной передачи с любыми другими типами зубчатых передач под использование их в качестве редуктора, таковыми особенностями являются: соосность входящего и исходящего потока мощности (например, валов) даже на однорядной планетарной передаче; возможность выбора из шести передаточных отношений даже на простой трёхзвенной планетарной передаче; две степени свободы любой планетарной передачи; возможность получения больших передаточных отношений в условиях ограниченного поперечного габарита.
Типы планетарных редукторов и их применение
Планетарный редуктор с одной степенью свободы
В таких редукторах опорное звено всегда заблокировано на корпус редуктора. При этом для любой трёхзвенной планетарной передачи возможны шесть вариантов распределения ролей между тремя основными звеньями, что даёт шесть передаточных отношений, три из которых могут применяться для редукторов (передаточное отношение больше единицы) и три для мультипликаторов (передаточное отношение меньше единицы).
Наиболее глубокую редукцию в схеме СВЭ даёт вариант 1 (с солнечной шестерни на водило), наиболее слабую — вариант 3 (с коронной шестерни на водило). Некое промежуточное значение редукции с обязательным противовращением даёт Вариант 5 (с солнечной шестерни на коронную), но в силу разных причин его используют не часто (единственный известный пример — колёсные редукторы дорожных автомобилей МАЗ). Оставшиеся три варианта дают мультипликацию, в том числе одно передаточное отношение обратного вращения.
Планетарные редукторы с одной степенью свободы применяются в бортовых главных передачах гусеничных машин, в двухступенчатых главных передачах колёсных грузовых машин в ступицах ведущих колёс, в грузовых лебёдках и тельферах, в автомобильных стартёрах, в совмещённых планетарных мотор-редукторах. Общий принцип применения — требование компактности редуктора и соосности ведущего и ведомого валов. В грузовых лебёдках и тельферах могут применяться двух- и трёхрядные планетарные передачи, а общее передаточное отношение таких планетарных редукторов может быть порядка 100.
Планетарный редуктор с двумя степенями свободы
Конструктивно подобный планетарный редуктор может быть аналогичен планетарному редуктору с одной степенью свободы, с тем лишь отличием, что опорное звено здесь может быть разблокировано. При этом планетарная передача перестаёт выполнять редукцию и становится дифференциалом, а ввиду того, что в любом дифференциале мощность на ведомых звеньях выравнивается до минимально востребованной на любом из двух этих звеньев, настоящее ведомое звено перестаёт передавать сколь-либо существенную мощность по кинематической цепи трансмиссии и останавливается, а вращается только разблокированное опорное звено. К подобным редукторам относится термин «дифференциальный редуктор».
Применяются в однорадиусных механизмах поворота гусеничных машин, где они одновременно выполняют функцию редукции и обеспечивают возможность плавного разрыва потока мощности. Также могут применяться везде, где требуется опция отключения потока мощности без необходимости остановки мотора или вала привода ведущего звена.
Многоскоростной планетарный редуктор
Многоскоростные планетарные редукторы допускают переключение между различными кинематическими цепями внутри себя, то есть, дают возможность использования разных передаточных отношений. Конструктивно это всегда реализуется через применение так называемых управляющих элементов: тормозов, блокировочных фрикционов, обгонных муфт. Наличие шести передаточных отношений даже на одном простом планетарном механизме теоретически допускает его использование в качестве минимально возможного, но фактически все многоскоростные планетарные редукторы выполнены либо на основе одного сложного планетарного механизма, либо на основе нескольких последовательно зацепленных простых (и сложных) планетарных механизмов. Число степеней свободы таких редукторов может быть 2 и более, общее число управляющих элементов может быть более десяти. Все многоскоростные планетарные редукторы имеют ту особенность, что взаимная блокировка их звеньев превращает их в прямую передачу, что может быть также использовано для расширения числа доступных скоростей.
В основном применяются в трансмиссиях транспортных машин: в двухрадиусных механизмах поворота гусеничных машин, в коробках передач и раздаточных коробках колёсных и гусеничных машин, где могут выполнять как функции делителя, овердрайва, ходоуменьшителя, так и функции основного набора передач включая реверс, независимо от общего числа скоростей. Также применяются в электроинструментах, где требуется возможность получения более одной скорости вращения.
Шарикоподшипниковый редуктор
Шарикоподшипник представляет пример планетарного редуктора, в котором водилом является сепаратор, функции солнечной шестерни выполняет внутреннее кольцо, функции коронной шестерни — наружное кольцо, а сателлиты — это шарики. С использованием обыкновенных шарикоподшипников могут быть сконструированы маломощные редукторы (для научных или измерительных приборов). Например, шарикоподшипниковые планетарные редукторы используются в конструкции верньера, применяемого для точной настройки радиостанции на нужную частоту приема/передачи.
См. также
Примечания
Ссылки
Дифференциальный редуктор
Изобретение относится к машиностроению, а именно к механическим передачам. Дифференциальный редуктор содержит корпус, размещенные в нем зубчатые шестерню и колесо с внешними и внутренними зубьями, расположенные на одной геометрической оси, входящие в зацепление с внешними зубьями промежуточных шестерней, установленных посредством осей на корпусе редуктора. Также редуктор содержит центральные шестерню и колесо с внешними и внутренними зубьями, входящие в зацепление с внешними зубьями сателлитов, установленных посредством осей на ведомом водиле. Причем центральное колесо с внутренними зубьями соединено с зубчатым колесом с внутренними зубьями, которое входит в зацепление с промежуточными шестернями с внешними зубьями, установленными посредством осей на корпусе редуктора, которые также входят в зацепление с шестерней с внешними зубьями, расположенной на ведущем валу, как и центральная шестерня с внешними зубьями. Достигается упрощение конструкции. 2 ил.
Изобретение относится к машиностроению, а именно к механическим передачам. Изобретение может найти применение во всех отраслях промышленности, где имеется потребность в увеличении крутящих моментов и преобразовании угловых скоростей.
Известен двухступенчатый планетарный редуктор, выполненный по схеме 2K-H, с двумя центральными колесами и двухвенцовыми сателлитами [1, стр.149, рис.5.27], [2, стр.226, схема 4, стр.281]. Ведущим является центральное колесо с внешним зацеплением, центральное колесо с внутренним зацеплением неподвижное, водило является ведомым. Передача обладает высоким к.п.д.
Недостатком данного редуктора является ограниченный диапазон передаточных чисел до u=17…19.
Известен двухступенчатый планетарный редуктор, выполненный по схеме 2K-H [1, стр.149, рис.5.26], [2, стр.228, схема 1, стр.236]. Каждая ступень редуктора состоит из двух центральных колес, одно из которых (с внешними зубьями) ведущее, а другое (с внутренними зубьями) неподвижное, и ведомого водила.
Недостатком данного редуктора являются сложность конструкции и ограниченность выбора передаточных чисел. Оптимальный диапазон передаточных чисел u=12…50, при этом к.п.д. снижается по сравнению с одноступенчатыми планетарными редукторами до значения 0,8.
Известен планетарный редуктор с тремя центральными колесами, выполненный по схеме 3K [1, стр.149, рис.5.28], [2, стр.227, схема 3]. Редуктор содержит три центральных колеса, из которых одно (с внешними зубьями) ведущее, другое (с внутренними зубьями) неподвижное, третье (с внутренними зубьями) соединено с выходным валом, водило не нагружено вращающим моментом. Оптимальный диапазон передаточных чисел u=30…250.
Недостатком данного редуктора являются сложность конструкции, недостаточный диапазон выбора передаточных чисел и пониженный к.п.д. — до 0,3 при больших передаточных числах.
Наиболее близким к предлагаемому изобретению является одноступенчатый планетарный редуктор, выполненный по схеме 2K-H [1, стр.148, рис.5.25], [2, стр.226, схема 1, стр.230], имеющий два центральных колеса, одно из которых (с внешними зубьями) ведущее, другое (с внутренними зубьями) соединено с корпусом — неподвижное, и ведомое водило с тремя сателлитами.
Недостатком данного редуктора при высоком к.п.д. 0,95…0,98 являются малые значения и ограниченный диапазон передаточных чисел U=3…9.
Данный механизм выбран в качестве прототипа.
Технический результат — создание механической передачи (редуктора) нового типа с диапазоном передаточных чисел от 1,678 до 12646 и более, с постоянным к.п.д., равным 0,94…0,97, исключающей необходимость изготовления дополнительных ступеней передачи, а также получение максимально большого количества промежуточных значений передаточных чисел в указанном диапазоне.
Технический результат достигается тем, что дифференциальный редуктор, содержащий корпус, размещенные в нем зубчатые шестерню и колесо с внешними и внутренними зубьями, расположенные на одной геометрической оси, входящие в зацепление с внешними зубьями промежуточных шестерней, установленных посредством осей на корпусе редуктора, и центральные шестерня и колесо с внешними и внутренними зубьями, входящие в зацепление с внешними зубьями сателлитов, установленных посредством осей на ведомом водиле, согласно изобретению центральное колесо с внутренними зубьями соединено с зубчатым колесом с внутренними зубьями, которое входит в зацепление с промежуточными шестернями с внешними зубьями, установленными посредством осей на корпусе редуктора, которые также входят в зацепление с шестерней с внешними зубьями, расположенной на ведущем валу, как и центральная шестерня с внешними зубьями.
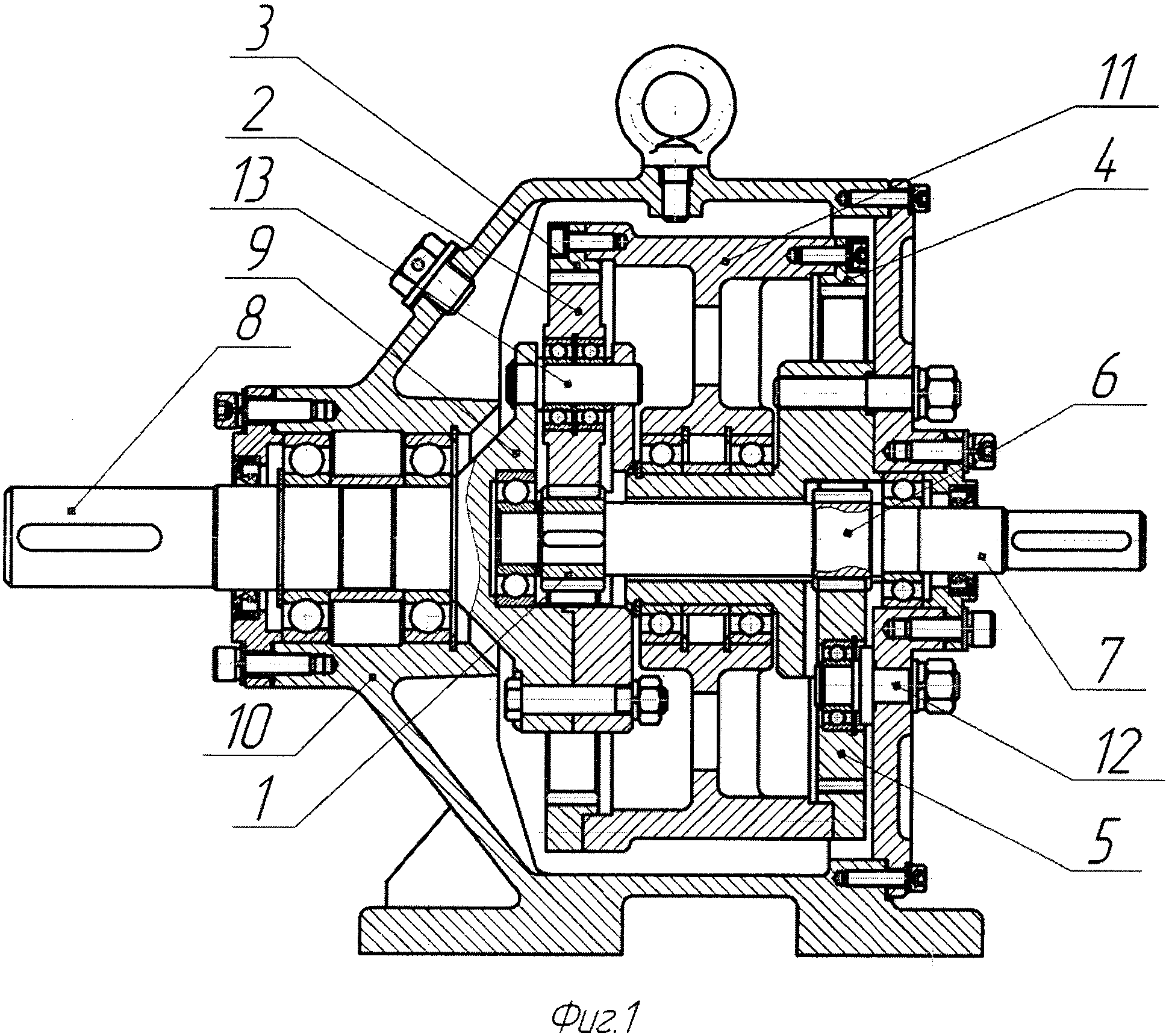
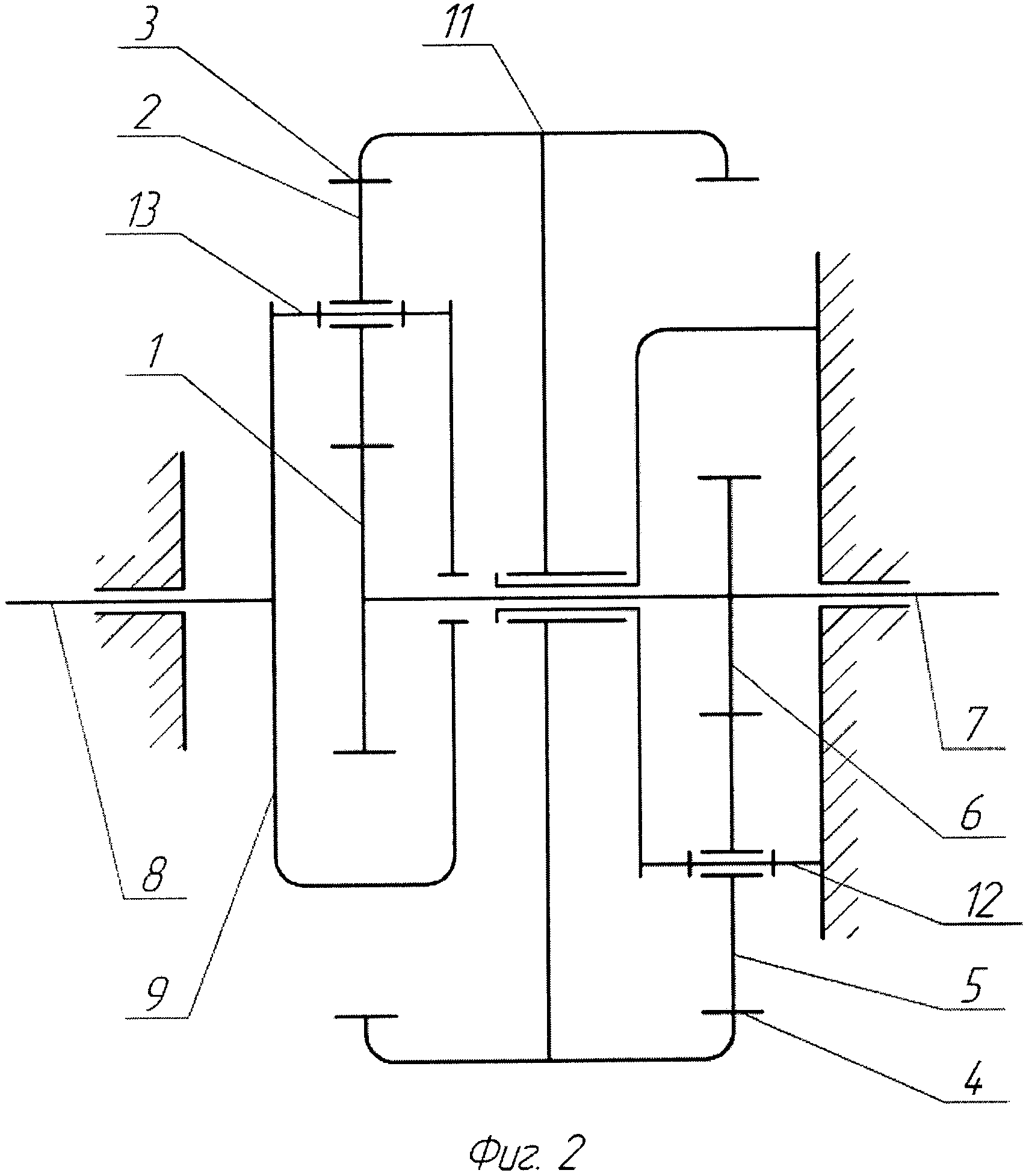
Конструкция редуктора поясняется чертежом и схемой. На фиг.1 показан продольный разрез редуктора, на фиг.2 показана кинематическая схема, соответствующая чертежу.
На чертежах обозначено: 1 — ведущая центральная шестерня с внешними зубьями, 2 — сателлиты, 3 — центральное колесо с внутренними зубьями, 4 — зубчатое колесо с внутренними зубьями, 5 — промежуточные шестерни с внешними зубьями, 6 — ведущая зубчатая шестерня с внешними зубьями, 7 — ведущий вал, 8 — выходной вал, 9 — водило, 10 — корпус редуктора, 11 — корпус колес 3 и 4, 12 — оси промежуточных шестерней 5, 13 — оси сателлитов 2.
Дифференциальный редуктор собран в корпусе 10, в полости которого расположен ведущий вал 7 с установленными на нем шестернями 1 и 6. Шестерня 6 входит в зацепление с промежуточными шестернями 5, установленными на корпусе при помощи осей 12, а шестерня 1 входит в зацепление с сателлитами 2, установленными на водиле 9 с помощью осей 13. Центральное колесо 3 и зубчатое колесо 4 установлены в корпусе 11, расположенном на одной геометрической оси с валом 7. Центральное колесо 3 входит в зацепление с сателлитами 2, а зубчатое колесо 4 — с промежуточными шестернями 5. Водило 9 соединено с выходным валом 8.
Дифференциальный редуктор работает следующим образом. Вращение ведущего вала 7 через зубчатую шестерню 6 воспринимается промежуточными шестернями 5, которые, входя в зацепление с зубчатым колесом 4 через корпус колес 11, вызывают противоположно направленное вращение центрального колеса 3. Одновременно вращение ведущего вала 7 через центральную шестерню 1 воспринимается сателлитами 2, которые, входя в зацепление с вращающимся центральным колесом 3, вызывают вращение водила 9, преобразуя частоту вращения и момент ведущего вала 7 до необходимых значений на выходном валу 8.
Передаточное число редуктора определяется по формуле:
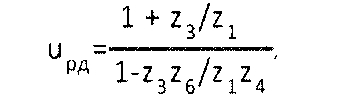
где z1, z3, z4, z6 — число зубьев шестерен 1, 6 и колес 3, 4 соответственно.
К.п.д. редуктора определяется по формуле:
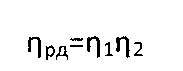
где η1 — к.п.д. планетарной передачи, выполненной по схеме 2K-H с одновенцовыми сателлитами и неподвижным водилом [2, стр.226, схема 3], которую образуют зубчатая шестерня 6, промежуточные шестерни 5, оси 12, зубчатое колесо 4, корпус редуктора 10;
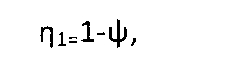
η2 — к.п.д. планетарной передачи, выполненной по схеме 2K-H с одновенцовыми сателлитами и невращающимся эпициклом [2, стр.226, схема 1], которую образуют центральная шестерня 1, сателлиты 2, оси сателлитов 13, центральное колесо 3 и водило 9;
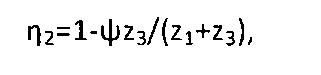
где ψ — коэффициент потерь простой передачи, равный 0,015…0,04.
Таким образом, посредством определенного подбора центральных и зубчатых шестерней и колес, промежуточных шестерней и сателлитов, отвечающего условиям собираемости передачи [1, стр.150-151], с количествами зубьев, находящихся в интервале значений от 14 до 125 включительно, достигается получение механической передачи (редуктора) с диапазонами передаточных чисел 1,678…12646 и к.п.д. 0,94…0,97, с количеством промежуточных значений передаточных чисел 3 261 636.
Источники информации
1. Иванов М.Н. и Иванов В.Н. Детали машин. Курсовое проектирование. Учеб. пособие для машиностроит. вузов. М.: «Высшая школа», 1975. — 551 с. с ил.
2. Анфимов М.И. Редукторы. Конструкции и расчет: Альбом. — 4-е изд., перераб. и доп. — М.: Машиностроение, 1993. — 464 с.: ил.
Дифференциальный редуктор, содержащий корпус, размещенные в нем зубчатые шестерню и колесо с внешними и внутренними зубьями, расположенные на одной геометрической оси, входящие в зацепление с внешними зубьями промежуточных шестерней, установленных посредством осей на корпусе редуктора, и центральные шестерню и колесо с внешними и внутренними зубьями, входящие в зацепление с внешними зубьями сателлитов, установленных посредством осей на ведомом водиле, отличающийся тем, что центральное колесо с внутренними зубьями соединено с зубчатым колесом с внутренними зубьями, которое входит в зацепление с промежуточными шестернями с внешними зубьями, установленными посредством осей на корпусе редуктора, которые также входят в зацепление с шестерней с внешними зубьями, расположенной на ведущем валу, как и центральная шестерня с внешними зубьями.
Дифференциальный редуктор
Изобретение относится к машиностроению, а именно к механическим передачам. Изобретение может найти применение во всех отраслях промышленности, где имеется потребность в увеличении крутящих моментов и преобразовании угловых скоростей.
Известен двухступенчатый планетарный редуктор, выполненный по схеме 2K-H, с двумя центральными колесами и двухвенцовыми сателлитами [1, стр.149, рис.5.27], [2, стр.226, схема 4, стр.281]. Ведущим является центральное колесо с внешним зацеплением, центральное колесо с внутренним зацеплением неподвижное, водило является ведомым. Передача обладает высоким к.п.д.
Недостатком данного редуктора является ограниченный диапазон передаточных чисел до u=17…19.
Известен двухступенчатый планетарный редуктор, выполненный по схеме 2K-H [1, стр.149, рис.5.26], [2, стр.228, схема 1, стр.236]. Каждая ступень редуктора состоит из двух центральных колес, одно из которых (с внешними зубьями) ведущее, а другое (с внутренними зубьями) неподвижное, и ведомого водила.
Недостатком данного редуктора являются сложность конструкции и ограниченность выбора передаточных чисел. Оптимальный диапазон передаточных чисел u=12…50, при этом к.п.д. снижается по сравнению с одноступенчатыми планетарными редукторами до значения 0,8.
Известен планетарный редуктор с тремя центральными колесами, выполненный по схеме 3K [1, стр.149, рис.5.28], [2, стр.227, схема 3]. Редуктор содержит три центральных колеса, из которых одно (с внешними зубьями) ведущее, другое (с внутренними зубьями) неподвижное, третье (с внутренними зубьями) соединено с выходным валом, водило не нагружено вращающим моментом. Оптимальный диапазон передаточных чисел u=30…250.
Недостатком данного редуктора являются сложность конструкции, недостаточный диапазон выбора передаточных чисел и пониженный к.п.д. — до 0,3 при больших передаточных числах.
Наиболее близким к предлагаемому изобретению является одноступенчатый планетарный редуктор, выполненный по схеме 2K-H [1, стр.148, рис.5.25], [2, стр.226, схема 1, стр.230], имеющий два центральных колеса, одно из которых (с внешними зубьями) ведущее, другое (с внутренними зубьями) соединено с корпусом — неподвижное, и ведомое водило с тремя сателлитами.
Недостатком данного редуктора при высоком к.п.д. 0,95…0,98 являются малые значения и ограниченный диапазон передаточных чисел U=3…9.
Данный механизм выбран в качестве прототипа.
Технический результат — создание механической передачи (редуктора) нового типа с диапазоном передаточных чисел от 1,678 до 12646 и более, с постоянным к.п.д., равным 0,94…0,97, исключающей необходимость изготовления дополнительных ступеней передачи, а также получение максимально большого количества промежуточных значений передаточных чисел в указанном диапазоне.
Технический результат достигается тем, что дифференциальный редуктор, содержащий корпус, размещенные в нем зубчатые шестерню и колесо с внешними и внутренними зубьями, расположенные на одной геометрической оси, входящие в зацепление с внешними зубьями промежуточных шестерней, установленных посредством осей на корпусе редуктора, и центральные шестерня и колесо с внешними и внутренними зубьями, входящие в зацепление с внешними зубьями сателлитов, установленных посредством осей на ведомом водиле, согласно изобретению центральное колесо с внутренними зубьями соединено с зубчатым колесом с внутренними зубьями, которое входит в зацепление с промежуточными шестернями с внешними зубьями, установленными посредством осей на корпусе редуктора, которые также входят в зацепление с шестерней с внешними зубьями, расположенной на ведущем валу, как и центральная шестерня с внешними зубьями.
Конструкция редуктора поясняется чертежом и схемой. На фиг.1 показан продольный разрез редуктора, на фиг.2 показана кинематическая схема, соответствующая чертежу.
На чертежах обозначено: 1 — ведущая центральная шестерня с внешними зубьями, 2 — сателлиты, 3 — центральное колесо с внутренними зубьями, 4 — зубчатое колесо с внутренними зубьями, 5 — промежуточные шестерни с внешними зубьями, 6 — ведущая зубчатая шестерня с внешними зубьями, 7 — ведущий вал, 8 — выходной вал, 9 — водило, 10 — корпус редуктора, 11 — корпус колес 3 и 4, 12 — оси промежуточных шестерней 5, 13 — оси сателлитов 2.
Дифференциальный редуктор собран в корпусе 10, в полости которого расположен ведущий вал 7 с установленными на нем шестернями 1 и 6. Шестерня 6 входит в зацепление с промежуточными шестернями 5, установленными на корпусе при помощи осей 12, а шестерня 1 входит в зацепление с сателлитами 2, установленными на водиле 9 с помощью осей 13. Центральное колесо 3 и зубчатое колесо 4 установлены в корпусе 11, расположенном на одной геометрической оси с валом 7. Центральное колесо 3 входит в зацепление с сателлитами 2, а зубчатое колесо 4 — с промежуточными шестернями 5. Водило 9 соединено с выходным валом 8.
Дифференциальный редуктор работает следующим образом. Вращение ведущего вала 7 через зубчатую шестерню 6 воспринимается промежуточными шестернями 5, которые, входя в зацепление с зубчатым колесом 4 через корпус колес 11, вызывают противоположно направленное вращение центрального колеса 3. Одновременно вращение ведущего вала 7 через центральную шестерню 1 воспринимается сателлитами 2, которые, входя в зацепление с вращающимся центральным колесом 3, вызывают вращение водила 9, преобразуя частоту вращения и момент ведущего вала 7 до необходимых значений на выходном валу 8.
Передаточное число редуктора определяется по формуле:
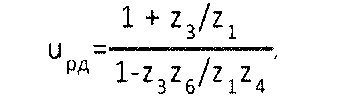
где z1, z3, z4, z6 — число зубьев шестерен 1, 6 и колес 3, 4 соответственно.
К.п.д. редуктора определяется по формуле:
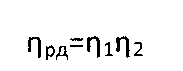
где η1 — к.п.д. планетарной передачи, выполненной по схеме 2K-H с одновенцовыми сателлитами и неподвижным водилом [2, стр.226, схема 3], которую образуют зубчатая шестерня 6, промежуточные шестерни 5, оси 12, зубчатое колесо 4, корпус редуктора 10;
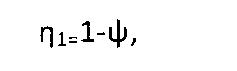
η2 — к.п.д. планетарной передачи, выполненной по схеме 2K-H с одновенцовыми сателлитами и невращающимся эпициклом [2, стр.226, схема 1], которую образуют центральная шестерня 1, сателлиты 2, оси сателлитов 13, центральное колесо 3 и водило 9;
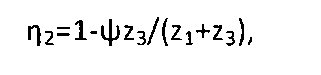
где ψ — коэффициент потерь простой передачи, равный 0,015…0,04.
Таким образом, посредством определенного подбора центральных и зубчатых шестерней и колес, промежуточных шестерней и сателлитов, отвечающего условиям собираемости передачи [1, стр.150-151], с количествами зубьев, находящихся в интервале значений от 14 до 125 включительно, достигается получение механической передачи (редуктора) с диапазонами передаточных чисел 1,678…12646 и к.п.д. 0,94…0,97, с количеством промежуточных значений передаточных чисел 3 261 636.
Источники информации
1. Иванов М.Н. и Иванов В.Н. Детали машин. Курсовое проектирование. Учеб. пособие для машиностроит. вузов. М.: «Высшая школа», 1975. — 551 с. с ил.
2. Анфимов М.И. Редукторы. Конструкции и расчет: Альбом. — 4-е изд., перераб. и доп. — М.: Машиностроение, 1993. — 464 с.: ил.
Дифференциальный редуктор, содержащий корпус, размещенные в нем зубчатые шестерню и колесо с внешними и внутренними зубьями, расположенные на одной геометрической оси, входящие в зацепление с внешними зубьями промежуточных шестерней, установленных посредством осей на корпусе редуктора, и центральные шестерню и колесо с внешними и внутренними зубьями, входящие в зацепление с внешними зубьями сателлитов, установленных посредством осей на ведомом водиле, отличающийся тем, что центральное колесо с внутренними зубьями соединено с зубчатым колесом с внутренними зубьями, которое входит в зацепление с промежуточными шестернями с внешними зубьями, установленными посредством осей на корпусе редуктора, которые также входят в зацепление с шестерней с внешними зубьями, расположенной на ведущем валу, как и центральная шестерня с внешними зубьями.