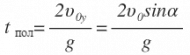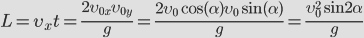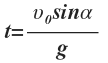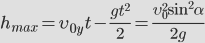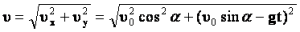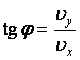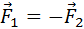| Движение тела, брошенного горизонтально или под углом к горизонту. | |
| |
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное. | |
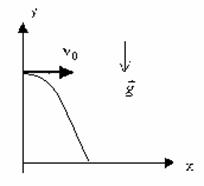
Движение тела, брошенного горизонтально. | |
Выразим проекции скорости и координаты через модули векторов. 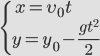
|  |
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y: | |
Движение тела, брошенного под углом к горизонту. | |
Порядок решения задачи аналогичен предыдущей. Решим задачу для случая х0=0 и y0=0. | 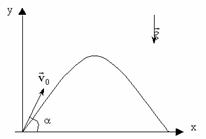 |
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории): Мы получили квадратичную зависимость между координатами. Значит траектория — парабола. | |
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0. Следовательно, для решения этой задачи необходимо решить уравнение | Время полета:
|
Зная время полета, найдем максимальное расстояние, которое пролетит тело: | Дальность полета: 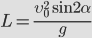
|
Из этой формулы следует, что: — максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450; — на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории. | 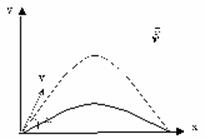 |
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело. 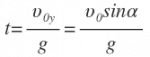 | Время подъема: |
Тогда: | 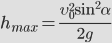
|
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна | |
Угол, под которым направлен вектор скорости в любой момент времени: | |
Движение тела, брошеного под углом к горизонту
При решении задач с телом, брошенным под углом к горизонту, очень важно помнить, что это движение состоит из двух: тело летит горизонтально, и его скорость постоянна, и одновременно тело сначала взлетает, а потом падает, и движение в вертикальной плоскости является сначала равнозамедленным, а потом равноускоренным. Кроме того, помогает то, что в высшей точке полета вертикальная составляющая скорости тела обращается в ноль. Если всегда помнить про этот факт – не проблема решить любую задачу.
Задача 1. Два тела брошены под углом и к горизонту с одинаковой начальной скоростью. Найти отношение дальностей полета тел и максимальных высот подъема.
Для первого тела максимальная высота подъема:
В наивысшей точке траектории вертикальная составляющая скорости равна нулю:
Время полета тела до апогея:
Тогда максимальная высота:
Аналогично для второго тела:
Таким образом, отношение высот подъема равно:
Теперь займемся дальностями полетов тел. Тело будет лететь по горизонтали с постоянной скоростью в течение времени и пролетит в итоге , где :
Аналогично для второго тела:
Определим отношение длин полетов:
Ответ: , .
Задача 2. Какой начальной скоростью должна обладать сигнальная ракета, выпущенная под углом к горизонту, чтобы она вспыхнула в наивысшей точке своей траектории? Время горения запала ракеты 6 с.
В наивысшей точке траектории вертикальная составляющая скорости равна нулю:
Отсюда можно определить скорость:
Ответ: 85 м/с
Задача 3. Два тела брошены с земли под углами и к горизонту из одной точки. Каково отношение сообщенных им начальных скоростей , если тела упали на землю также в одной точке?
К задаче 3
Время полета первого тела до верхней точки:
Полное время полета:
Вертикальная составляющая скорости тела:
Горизонтальная составляющая:
Дальность полета тела:
Аналогично для второго тела:
Время полета второго тела до верхней точки:
Полное время полета:
Вертикальная составляющая скорости тела:
Горизонтальная составляющая:
Дальность полета тела:
Возьмем отношение дальностей и приравняем к 1, так как тела шлепнулись в одном месте:
Ответ: .
Задача 4. Мальчик бросает мяч со скоростью м/с под углом в в сторону стены, стоя на расстоянии 4 м от нее. На каком расстоянии от стены должен встать мальчик, чтобы поймать мяч? Удар мяча о стенку считать абсолютно упругим.
К задаче 4
Сначала выясним, в каком месте траектории находился мяч, когда ударился о стенку: был ли он на первой ее половине, или же он уже прошел точку максимального подъема? От этого зависит угол, под которым мяч подлетел к стенке, а раз удар абсолютно упругий, значит, мячик и отскочил под этим же углом. Поэтому сначала найдем середину траектории мяча, как если бы стенки не было.
Время полета мяча до верхней точки:
Вертикальная составляющая скорости мяча:
Горизонтальная составляющая:
Дальность полета мяча до верхней точки траектории:
Итак, мячик не долетел до верхней точки траектории, теперь можно изобразить стенку и траекторию полета мяча:
Отскок мяча
Из рисунка видно, что, поскольку угол падения равен углу отражения, то траектория отскока мячика будет полностью повторять его траекторию полета без стенки, только в виде отражения:
Как мы выяснили ранее, мячику лететь до верхней точки траектории 5 м, значит, всего он пролетел бы 10 метров, но стенка помешала. Траектория оказалась разбита ею на два куска: 4 и 6 м, 4 до стенки, и 6 – после отскока. Таким образом, мальчику надо отступить на 2 метра, чтобы поймать мяч.
Ответ: отступить на 2 м, расстояние от стены – 6 м.
Задача 5. Тело брошено со скоростью 20 м/с под углом к горизонту. Найти координаты точек траектории тела, в которых вектор скорости составляет с горизонтом угол , если начало координат – точка бросания тела?
Горизонтальная составляющая скорости тела сохраняется постоянной на всем пути, она равна . Скорость будет составлять угол в с горизонтом только тогда, когда вертикальная составляющая скорости будет равна горизонтальной составляющей по модулю, так как скорость может составлять с горизонтом как положительный, так и отрицательный угол – когда тело уже прошло верхнюю точку траектории и снижается. То есть подходящих нам точек траектории у тела 2: на взлете и при падении.
К задаче 5
Тогда:
Это произойдет в момент времени, равный:
Очевидно, что координата тела по оси не будет отличаться для обеих точек. Найдем ее:
Координату по оси первой точки (на взлете) найдем, подставив известное время в формулу движения с постоянной скоростью:
Координата второй точки по оси получится, если найденное только что расстояние вычесть из полного пути, пройденного телом – ведь точки расположены на траектории симметрично. Полный путь тело пройдет за полное время движения, а оно равно удвоенному времени взлета:
Тогда искомая координата:
Теперь давайте все это посчитаем:
Ответ: м, м, м.
Задача 6. С вершины горы бросают камень под углом к горизонту. Определить начальную скорость камня, если он упал на расстоянии 20 м от точки бросания. Угол наклона горы к горизонту также .
К задаче 6
Удобно ввести систему координат так, чтобы ось совпадала со склоном горы, а ось была бы направлена перпендикулярно склону. Тогда, в такой системе координат, тело будет двигаться с ускорением как по оси , так и по оси . Начальная скорость тела будет направлена под углом к склону, и ее можно разложить на составляющие:
Таким же образом разложим и ускорение свободного падения:
Когда тело доберется до верхней точки траектории, его вертикальная составляющая скорости обратится в ноль:
Откуда найдем время полета до верхней точки:
Полное время полета – вдвое больше:
За полное время тело, двигаясь равноускоренно, пролетит вдоль оси расстояние:
По условию , поэтому
Ответ: м/с
Задача 7. Из пушки выпустили последовательно 2 снаряда со скоростью м/с: первый – под углом к горизонту, второй – под углом (азимут один и тот же). Найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.
К задаче 7
Чтобы снаряды столкнулись в воздухе, а произойти это может только на второй половине траектории при заданных углах, нужно, чтобы были равны координаты снарядов по оси и по оси .
Раскладываем скорости по осям:
Из условия равенства нулю вертикальной составляющей скорости получаем половинку времени полета первого снаряда:
Полное время полета первого снаряда:
Полное время полета второго снаряда:
Снаряды будут лететь по оси с постоянной скоростью, и пролетят
Первый:
Второй:
Так как их координаты равны, то приравняем:
Откуда получаем соотношение:
По оси первый снаряд пролетит:
Второй снаряд пролетит:
Приравняем:
Заменим на :
Сокращаем:
Получим время :
Отсюда время :
И разность времен:
Ответ: 10,56 с
Закон всемирного тяготения. Движение тел под действием силы тяжести
По второму закону Ньютона причиной изменения движения, т. е. причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения.
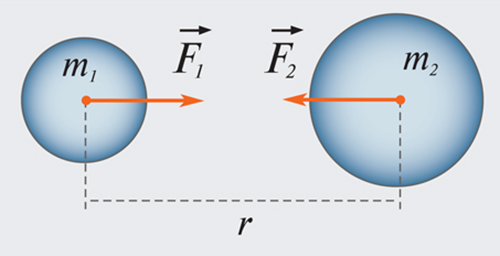
Закон всемирного тяготения был открыт Исааком Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс (рис. 1.10.1). Понятие центра масс тела будет строго определено в 1.23.
У однородного шара центр масс совпадает с центром шара.
|
Рисунок 1.10.1. Гравитационные силы притяжения между телами.
|
В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом Иоганном Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
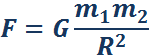
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной
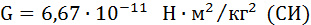
Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, R – ее радиус, m – масса данного тела, то сила тяжести равна
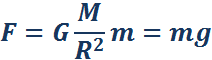
где g – ускорение свободного падения у поверхности Земли:
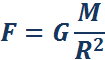
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения.
Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (R = 6,38·106 м), можно вычислить массу Земли М:
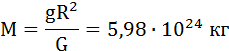
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт весом 71,5 кг (Гагарин) притягивается к Земле вблизи ее поверхности равна 700 Н.
|
Рисунок 1.10.2. Изменение силы тяготения, действующей на космонавта при удалении от Земли |
Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет
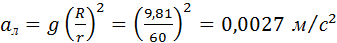
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения:
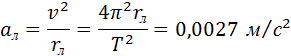
где T = 27,3 сут – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.
Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gЛ определится выражением:
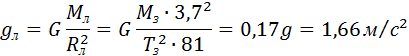
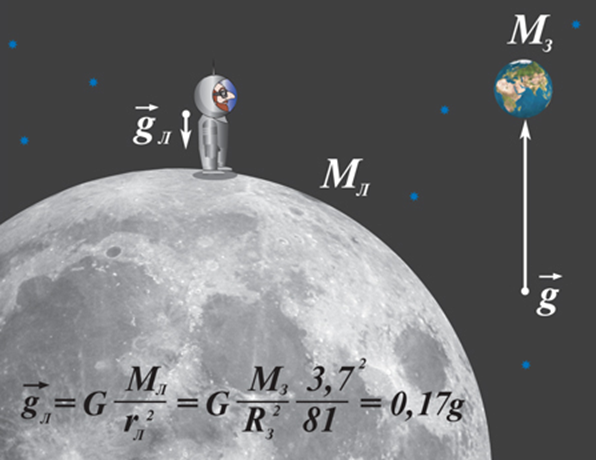
В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.
Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим:
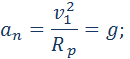
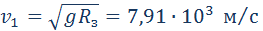
Двигаясь с такой скоростью, спутник облетал бы Землю за время
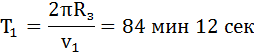
На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли.
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия
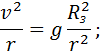
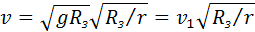
Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.
Период T обращения такого спутника равен

Здесь T1 – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 RЗ называется геостационарной.
Движение тела, брошенного под углом к горизонту | LAMPA
Как решать задачи
В задачах о теле, брошенном под углом к горизонту, чаще всего бывает нужно найти:
- время подъема на вершину tвершиныt_{вершины}tвершины;
- максимальную высоту подъема hhh;
- время падения на землю ttt;
- дальность полета LLL.
Если вы просматривали тему «Движение тела, брошенного вертикально вверх», то вы, наверно, уже догадались, каким образом находятся все эти величины. Для тех же, кто не догадался или же не читал ту тему, мы скажем, что для нахождения этих четырех величин используются особенности тех точек траектории, в которых надо найти время, координату и т.д. Главное слово — особенности. Чтобы было понятнее, рассмотрим нахождение этих величин на конкретном примере.
Условие
Из пушки вылетел снаряд с начальной скоростью V0=100V_0=100V0=100 м/с под углом к горизонту α=30∘\alpha=30^{\circ}α=30∘. Найдите:
- время подъема на вершину tвершиныt_{вершины}tвершины;
- максимальную высоту подъема hhh;
- время падения на землю ttt;
- дальность полета LLL.
Решение
Шаг 1. Сделаем что? Правильно — рисунок. Обозначим на нем оси.
Шаг 2. Запишем уравнения движения. Сначала в общем виде:
x=x0+V0xtx=x_0+V_{0x}tx=x0+V0xt,
Vx=V0x=V0cosα=constV_x=V_{0x}=V_0\cos\alpha=constVx=V0x=V0cosα=const,
y=y0+V0yt+ayt22y=y_0+V_{0y}t+\frac{a_yt^2}{2}y=y0+V0yt+2ayt2,
Vy=V0y+aytV_y=V_{0y}+a_ytVy=V0y+ayt,
V0y=V0sinαV_{0y}=V_0\sin\alphaV0y=V0sinα.
«Адаптируем» уравнения к нашему случаю:
x=V0xtx=V_{0x}tx=V0xt,
Vx=V0x=V0cosα=constV_x=V_{0x}=V_0\cos\alpha=constVx=V0x=V0cosα=const,
y=V0yt−gt22y=V_{0y}t-\frac{gt^2}{2}y=V0yt−2gt2,
Vy=V0y−gtV_y=V_{0y}-gtVy=V0y−gt,
V0y=V0sinαV_{0y}=V_0\sin\alphaV0y=V0sinα.
Подставим конкретные числовые значения:
x=100⋅cos30∘⋅tx=100\cdot \cos 30^{\circ}\cdot tx=100⋅cos30∘⋅t,
Vx=100⋅cos30∘V_x=100\cdot \cos 30^{\circ}Vx=100⋅cos30∘,
y=100⋅sin30∘⋅t−10t22y=100\cdot \sin 30^{\circ}\cdot t-\frac{10t^2}{2}y=100⋅sin30∘⋅t−210t2,
Vy=100⋅sin30∘−10tV_y=100\cdot \sin 30^{\circ}-10tVy=100⋅sin30∘−10t,
V0y=100⋅sin30∘V_{0y}=100\cdot \sin 30^{\circ}V0y=100⋅sin30∘.
Замечательно!
Шаг 3. Займемся временем подъема на вершину tвершиныt_{вершины}tвершины.
Движение тела под действием силы тяжести: определение, формулы
Движение тела под действием силы тяжести является одной из центральных тем в динамической физике. О том, что раздел динамики базируется на трех законах Ньютона, знает даже обычный школьник. Давайте постараемся разобрать эту тему досконально, а статья, подробно описывающая каждый пример, поможет нам сделать изучение движения тела под действием силы тяжести максимально полезным.
Немного истории
Испокон веков люди с любопытством наблюдали за различными явлениями, происходящими в нашей жизни. Человечество долгое время не могло понять принципы и устройство многих систем, однако длительный путь изучения окружающего мира привел наших предков к научному перевороту. В наши дни, когда технологии развиваются с неимоверной скоростью, люди почти не задумываются о том, каким образом работают те или иные механизмы.

А между тем наши предки всегда интересовались загадками природных процессов и устройством мира, искали ответы на самые сложные вопросы и не переставали изучать, пока не находили на них ответы. Так, например, известный ученый Галилео Галилей еще в 16 веке задался вопросами: «Почему тела всегда падают вниз, какая же сила притягивает их к земле?» В 1589 году он поставил ряд опытов, результаты которых оказались весьма ценными. Он подробно изучал закономерности свободного падения различных тел, сбрасывая предметы со знаменитой башни в городе Пизе. Законы, которые он вывел, были улучшены и более детально описаны формулами еще одним известным английским ученым — сэром Исааком Ньютоном. Именно ему принадлежат три закона, на которых основана практически вся современная физика.

Тот факт, что закономерности движения тел, описанные более 500 лет назад, актуальны и по сей день, означает, что наша планета подчиняется неизменным законам. Современному человеку необходимо хотя бы поверхностно изучить основные принципы обустройства мира.
Основные и вспомогательные понятия динамики
Для того чтобы полностью понять принципы подобного движения, следует сначала ознакомиться с некоторыми понятиями. Итак, самые необходимые теоретические термины:
- Взаимодействие — это воздействие тел друг на друга, при котором происходит изменение или начало их движения относительно друг друга. Различают четыре вида взаимодействия: электромагнитное, слабое, сильное и гравитационное.
- Скорость — это физическая величина, обозначающая быстроту, с которой двигается тело. Скорость является вектором, то есть имеет не только значение, но также и направление.
- Ускорение — та величина, которая показывает нам быстроту изменения скорости тела в промежуток времени. Она также является векторной величиной.
- Траектория пути — это кривая, а иногда — прямая линия, которую очерчивает тело при движении. При равномерном прямолинейном движении траектория может совпадать со значением перемещения.
- Путь — это длина траектории, то есть ровно столько, сколько прошло тело за определенное количество времени.
- Инерциальная система отсчета — это среда, в которой выполняется первый закон Ньютона, то есть тело сохраняет свою инерцию, при условии, что полностью отсутствуют все внешние силы.
Вышеуказанных понятий вполне достаточно для того, чтобы грамотно начертить или представить в голове моделирование движения тела под действием силы тяжести.

Что значит сила?
Давайте перейдем к основному понятию нашей темы. Итак, сила — это величина, смысл которой заключается в воздействии или влиянии одного тела на другое количественно. А сила тяжести — это та сила, которая действует абсолютно на каждое тело, находящееся на поверхности или вблизи нашей планеты. Возникает вопрос: откуда же берется эта самая сила? Ответ заключается в законе всемирного тяготения.
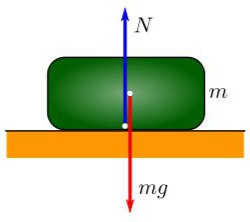
А что такое сила тяжести?
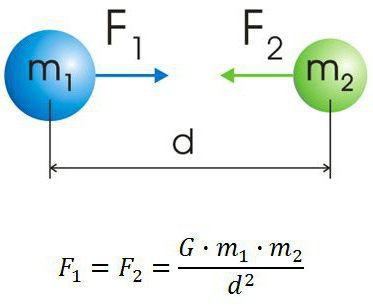
На любое тело со стороны Земли оказывает влияние гравитационная сила, которая сообщает ему некоторое ускорение. Сила тяжести всегда имеет вертикальное направление вниз, к центру планеты. Иначе говоря, сила тяжести притягивает предметы к Земле, вот почему предметы всегда падают вниз. Получается, что сила тяжести — это частный случай силы всемирного тяготения. Ньютон вывел одну из главных формул для нахождения силы притяжение между двумя телами. Выглядит она таким образом: F = G * (m1 хm2) / R2.
Чему равно ускорение свободного падения?
Тело, которое отпустили с некоторой высоты, всегда летит вниз под действием силы притяжения. Движение тела под действием силы тяжести вертикально вверх и вниз можно описать уравнениями, где основной константой будет являться значение ускорения «g». Эта величина обусловлена исключительно действием силы притяжения, и ее значение приблизительно равно 9,8 м/с2. Получается, что тело, брошенное с высоты без начальной скорости, будет двигаться вниз с ускорением равным значению «g».
Движение тела под действием силы тяжести: формулы для решения задач
Основная формула нахождения силы тяжести выглядит следующим образом: Fтяжести = m х g, где m — это масса тела, на которое действует сила, а «g» — ускорение свободного падения (для упрощения задач его принято считать равным 10 м/с2).
Есть еще несколько формул, используемых для нахождения того или иного неизвестного при свободном движении тела. Так, например, для того чтобы вычислить пройденный телом путь, необходимо подставить известные значения в эту формулу: S = V0 хt + a х t2 / 2 (путь равен сумме произведений начальной скорости умноженной на время и ускорения на квадрат времени, деленной на 2).
Уравнения для описания вертикального движения тела
Движение тела под действием силы тяжести по вертикали можно описать уравнением, которое выглядит так: x = x0 + v0 х t + a х t2 / 2. Используя данное выражение, можно найти координаты тела в известный момент времени. Необходимо просто подставить известные в задаче величины: начальное местоположение, начальную скорость (если тело не просто отпустили, а толкнули с некоторой силой) и ускорение, в нашем случае оно будет равно ускорению g.
Таким же образом можно найти и скорость тела, которое движется под действием силы притяжения. Выражение для нахождения неизвестной величины в любой момент времени: v = v0 + g х t (значение начальной скорости может быть равным нулю, тогда скорость будет равна произведению ускорения свободного падения на значение времени, за которое тело совершает движение).
Движение тел под действием силы тяжести: задачи и способы их решений
При решении многих задач, связанных с силой тяжести, рекомендуем воспользоваться следующим планом:
- Определить для себя удобную инерциальную систему отсчета, обычно принято выбирать Землю, потому как она отвечает многим требованиям к ИСО.
- Нарисовать небольшой чертеж или рисунок, на котором изображены основные силы, действующие на тело. Движение тела под действием силы тяжести подразумевает набросок или схему, на которой указано, в каком направлении движется тело, если на него действует ускорение, равное g.
- Затем следует выбрать направление для проецирования сил и полученных ускорений.
- Записать неизвестные величины и определить их направление.
- И наконец, используя указанные выше формулы для решения задач, вычислить все неизвестные величины, подставив данные в уравнения для нахождения ускорения или пройденного пути.
Готовое решение легкой задачи
Когда речь идет о таком явлении, как движение тела под действием силы тяжести, определение того, каким способом практичнее решать поставленную задачу, может быть затруднительным. Однако есть несколько хитростей, используя которые, можно с легкостью решить даже самое сложное задание. Итак, разберем на живых примерах, как следует решать ту или иную задачу. Начнем с легкой для понимания задачи.
Некоторое тело отпустили с высоты 20 м без начальной скорости. Определить, за какое количество времени оно достигнет поверхности земли.
Решение: нам известен путь, пройденный телом, известно, что начальная скорость была равна 0. Также можем определить, что на тело действует только сила тяжести, получается, что это движение тела под действием силы тяжести, и поэтому следует воспользоваться этой формулой: S = V0 хt + a х t2/2. Так как в нашем случае a = g, то после некоторых преобразований получаем следующее уравнение: S = g х t2 / 2. Теперь осталось только выразить время через эту формулу, получаем, что t2 = 2S / g. Подставим известные величины (при этом считаем, что g = 10 м/с2) t2 = 2 х 20 / 10 = 4. Следовательно, t = 2 с.
Итак, наш ответ: тело упадет на землю за 2 секунды.
Трюк, позволяющий быстро решить задачу, состоит в следующем: можно заметить, что описанное движение тела в приведенной задаче происходит в одном направлении (вертикально вниз). Оно весьма схоже с равноускоренным движением, так как на тело не действует никакая сила, кроме силы тяжести (силой сопротивления воздуха пренебрегаем). Благодаря этому можно воспользоваться легкой формулой для нахождения пути при равноускоренном движении, минуя изображения чертежей с расстановкой действующих на тело сил.
Пример решения более сложной задачи
А теперь давайте посмотрим, как лучше решать задачи на движение тела под действием силы тяжести, если тело движется не вертикально, а имеет более сложный характер перемещения.
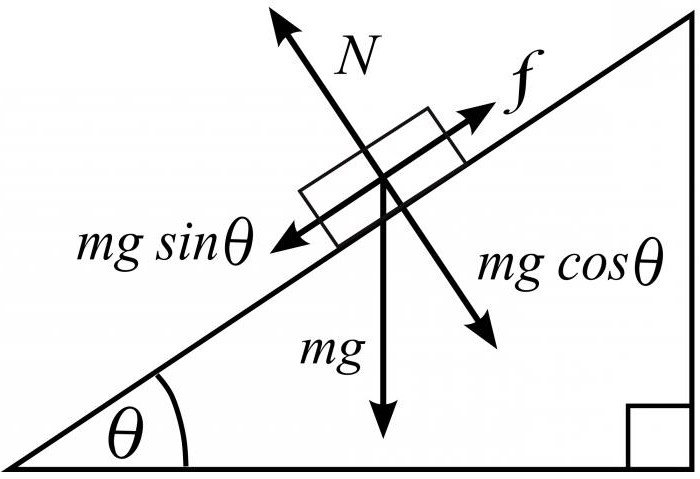
Например, следующая задача. Некоторый предмет массой m движется с неизвестным ускорением вниз по наклонной плоскости, коэффициент трения которой равен k. Определить значение ускорения, которое имеется при движении данного тела, если угол наклона α известен.
Решение: Следует воспользоваться планом, который описан выше. В первую очередь начертить рисунок наклонной плоскости с изображением тела и всех действующих на него сил. Получится, что на него действуют три составляющие: сила тяжести, трения и сила реакции опоры. Выглядит общее уравнение равнодействующих сил так: Fтрения + N + mg = ma.
Главной изюминкой задачи является условие наклонности под углом α. При проецировании сил на ось ox и ось oy необходимо учесть данное условие, тогда у нас получится следующее выражение: mg х sin α — Fтрения = ma (для оси ох) и N — mg х cos α = Fтрения (для оси oy).
Fтрения легко вычислить по формуле нахождения силы трения, она равна k х mg (коэффициент трения, умноженный на произведение массы тела и ускорения свободного падения). После всех вычислений остается только подставить найденные значения в формулу, получится упрощенное уравнение для вычисления ускорения, с которым движется тело вдоль наклонной плоскости.
Закон всемирного тяготения. Движение тел под действием силы тяжести
Исходя из трактовки второго закона Ньютона, можно сделать вывод, что изменение движения происходит посредствам силы. Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.
Закон всемирного тяготения. Формулы
В 1862 году был открыт закон всемирного тяготения И. Ньютоном. Он предположил, что силы, удерживающие Луну, той же природы, что и силы, заставляющие яблоко падать на Землю. Смысл гипотезы состоит в наличии действия сил притяжения, направленных по линии и соединяющих центры масс, как изображено на рисунке 1.10.1. Шаровидное тело имеет центр массы, совпадающий с центром шара.

Рисунок 1.10.1. Гравитационные силы притяжения между телами. F1→=-F2→.
Далее, Ньютон искал физическое объяснение законам движения планет, которые открыл И. Кеплер в начале XVII века, и давал количественное выражение для гравитационных сил.
Определение 1При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики.
Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача). Обратная же выполняется с определением действующих сил на тело с известным его направлением. Такие задачи привели ученого к открытию определения закона всемирного тяготения.
Ускорение свободного падения
Определение 2Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
F=Gm1m2r2.
Значение G определяет коэффициент пропорциональности всех тел в природе, называемое гравитационной постоянной и обозначаемое по формуле G=6,67·10-11 Н·м2/кг2 (СИ).
Большинство явлений в природе объясняются наличием действия силы всемирного тяготения. Движение планет, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все объясняется законом тяготения и динамики.
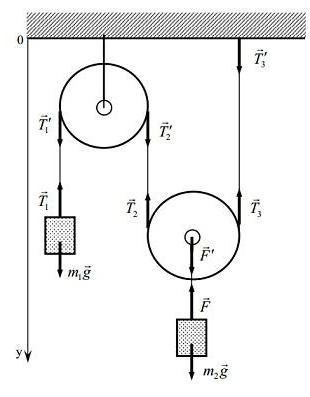
Движение тела под действием нескольких сил
Теоретически тела могут двигаться при воздействии на них одной силы: силы упругости, силы тяготения или силы трения. Но в реальности такие движения в земных условиях можно наблюдать очень редко. В большинстве случаев наряду с силами упругости и тяготения на тело всегда действует сила трения.
 При прямолинейном падении тела в жидкости или в газе на тело действует две силы – сила тяжести и сила сопротивления газа или жидкости.
При прямолинейном падении тела в жидкости или в газе на тело действует две силы – сила тяжести и сила сопротивления газа или жидкости.
Если пренебречь всеми другими силами, то можно считать, что в момент, когда падение тела только начинается (v = 0), на него действует только одна сила тяжести Fт. Сила сопротивления отсутствует. Но как только движение тела началось, сразу же появляется сила сопротивления – сила жидкого трения, которая растёт с увеличением скорости и направлена против неё.
Если сила тяжести остаётся постоянной, направленная в противоположную сторону сила сопротивления растёт вместе со скоростью тела, обязательно настанет тот момент, когда они по модулю станут равными друг другу. Как только это произойдёт, равнодействующая обеих сил станет равной нулю. Ускорение тела также станет равным нулю, и тело начнёт двигаться с постоянной скоростью.
Если тело падает в жидкости, кроме силы тяжести, необходимо учитывать и выталкивающую силу, направленную противоположно силе тяжести. Но так как эта сила постоянна и не зависит от скорости, то она не препятствует установлению постоянной скорости движения падающего тела.
Как решают задачи механики, если на тело действует несколько сил?
Вспомним второй закон Ньютона:
 где F – это векторная сумма всех сил, приложенных к телу. Векторное сложение сил можно заменить их алгебраическим сложением их проекций на координатные оси. При решении задач по механике, необходимо сначала изобразить на чертеже векторы всех сил, действующих не тело, и ускорения тела (если известно его направление). После выбора направления координатных осей, необходимо найти проекции всех векторов на эти оси. Далее нужно составить уравнение второго закона Ньютона для проекций на каждую ось и решить полученные скалярные уравнения.
где F – это векторная сумма всех сил, приложенных к телу. Векторное сложение сил можно заменить их алгебраическим сложением их проекций на координатные оси. При решении задач по механике, необходимо сначала изобразить на чертеже векторы всех сил, действующих не тело, и ускорения тела (если известно его направление). После выбора направления координатных осей, необходимо найти проекции всех векторов на эти оси. Далее нужно составить уравнение второго закона Ньютона для проекций на каждую ось и решить полученные скалярные уравнения.
Если в условиях задачи рассматривается движение нескольких тел, то уравнение второго закона Ньютона применяют к каждому телу отдельно и затем совместно решают полученные уравнения.
Решим задачу.
Брусок массой m движется по наклонной плоскости с углом α. Коэффициент трения бруска о плоскость µ. Найдите ускорение а бруска.
Для решения задачи необходимо построить чертёж и изобразить на нём векторы всех сил, действующих на брусок.

На брусок действуют три силы: сила тяжести Fт = mg, сила трения Fтр и сила реакции опоры N (сила упругости). Совместно эти силы сообщают бруску ускорение ā, которое направлено вниз вдоль плоскости.
Направим оси координат X параллельно наклонной плоскости, а ось координат Y перпендикулярно наклонной плоскости.
Вспомним второй закон Ньютона в векторной форме:

Для решения задачи нам необходимо записать это уравнение в скалярной форме. Для этого необходимо найти проекции векторов на оси X и Y .
Проекции на ось X. Проекция aх положительна и равна модулю вектора ā: aх = a. Проекция (Fт)х положительна и равна, как видно из треугольника АВD, mg sin α. Проекция (Fтр)х отрицательна и равна – Fтр. Проекция N вектора N равна нулю: Nх = 0. Уравнение второго закона Ньютона в скалярной форме записывается поэтому так:
ma = mg sin α – Fтр.
Проекциии на ось Y.Проекция aу равна нулю (вектор a перпендикулярен оси Y!): a = 0. Проекция (Fт)у отрицательна. Из треугольника ADC видно, что (Fт)у = -mg cos α. Проекция N положительна и равна модулю вектора Nу = N. Проекция (F) равна нулю: (Fтр)у = 0. Тогда уравнение второго закона Ньютона запишем так:
0 = N – mg cos α.
Откуда
N = mg cos α.
Сила трения по модулю равна µN, отсюда Fтр = µ mg cos α.
Подставим это выражение вместо силы трения в первое полученное скалярное уравнение:
ma = mg sin α – µ mg cos α;
a = g(sin α – µ cos α).
Ускорение a, меньше, чем g. Если трение отсутствует (µ = 0), то ускорение скользящего по наклонной плоскости тела равно по модулю g sin α, и в таком случае оно также меньше g.
На практике наклонные плоскости и используются как устройства, позволяющее уменьшить ускорение (g) при движении тела вниз или вверх.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.


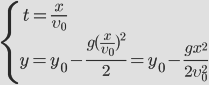 — между координатами квадратичная зависимость, траектория – парабола!
— между координатами квадратичная зависимость, траектория – парабола!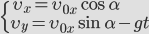

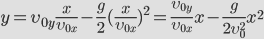
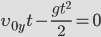 . Оно будет иметь решение при t=0 (начало движения) и
. Оно будет иметь решение при t=0 (начало движения) и