Рисунок рычага: Простые механизмы. Рычаг (Побединский Д.М.). Видеоурок. Физика 7 Класс – рычаг векторные изображения, графика и иллюстрации

Содержание

Простые механизмы. Рычаг (Побединский Д.М.). Видеоурок. Физика 7 Класс

На данном уроке речь пойдет о простых механизмах.

Простые механизмы – это устройства, с помощью которых работа совершается только за счет механической энергии. Нас окружают устройства, работающие за счет электроэнергии (см. рис. 1), за счет энергии сгорания топлива, но не всегда так было.

Рис. 1. Чайник, работающий за счет электроэнергии

Раньше всю работу можно было выполнить фактически руками, или с помощью животных, за счет ветра или течения воды (мельницы), то есть за счет механической энергии (см. рис. 2).

Рис. 2. Давние простые механизмы

И помогают в этом, облегчают выполнение работы, простые механизмы.

Наши силы ограничены, и это проблема. Мы, например, не можем за один раз поднять и перенести с одного места на другое тонну кирпичей. Зато мы можем потратить больше времени, пройти большее расстояние туда-сюда и перенести кирпичи по четыре за один подход, или сколько сможем унести. Как быть с шурупом, который нужно вкрутить в дерево? Вкрутить его голыми руками мы не можем. Вкрутить его по кусочку, как гору кирпичей по кирпичику, тоже нельзя. Нужно использовать механизм, отвертку. С ней нам приходится прокрутить шуруп на несколько оборотов, чтобы он вошёл в дерево хотя бы на сантиметр. Но зато это несравненно легче, чем руками.

Рассмотрим такой простой механизм, как, например, лопата. Конечно, она облегчает выполнение работы, с ней намного легче копать землю, чем руками. Мы воткнули лопату в землю. Чтобы поднять ком земли, нужно надавить на черенок. Где вы будете давить, чтобы было легче? Опыт подсказывает, что надо надавить, то есть приложить силу, поближе к концу черенка (см. рис. 3).

Рис. 3. Выбор точки приложения силы

Попробуйте приложить силу ближе к полотну лопаты, поднять ком земли станет намного тяжелее. Прикладывая прежнюю силу, вы уже ничего не поднимете. Именно поэтому лопаты с коротким черенком, например саперные, делаются с маленьким полотном: много земли с коротким черенком все равно не поднимешь.

Лопата представляет собой рычаг. Рычаг – это твердое тело, имеющее неподвижную ось вращения (чаще всего это точка опоры или подвеса). На него действуют силы, которые стремятся повернуть его вокруг оси вращения. У лопаты ось вращения – это точка опоры на верхнем краю ямки (см. рис. 4).

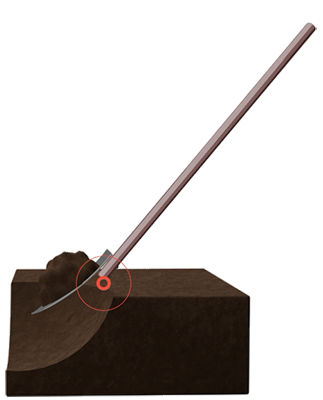
Рис. 4. Ось вращения лопаты

На полотно лопаты с некоторой силой действует комок земли, который мы поднимаем, а на черенок, с меньшей силой, – наши руки (см. рис. 5).

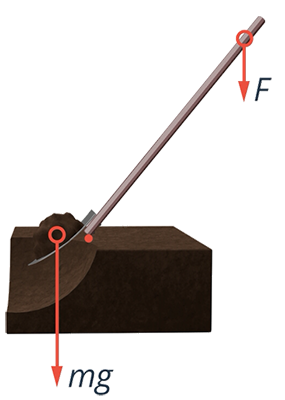
Рис. 5. Действие сил

Рассмотрим другой пример: все катались на качелях-балансире (см. рис. 6).

Рис. 6. Качели-балансир

Это тоже рычаг: есть неподвижная ось вращения, вокруг которой качели вращаются под действием сил тяжести детей.

Чтобы перевесить своего друга, сидящего на противоположном сидении, поднять его, вы сядете на самый край качели. Если сядете ближе к опоре качели, можете не перевесить. Тогда нужно на ваше место посадить кого-то взрослого и тяжелого (см. рис. 7).

Рис. 7. Приложенная сила должна быть больше, чем на краю

В такой точке приложения силы нужна большая сила, чем когда сила прикладывалась к краю качели (см. рис. 8).

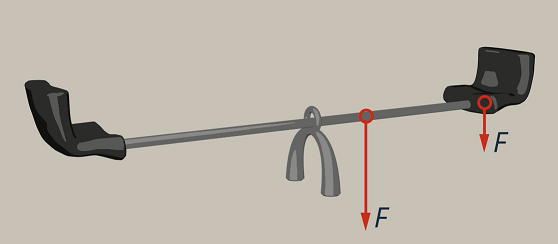
Рис. 8. Приложение сил

Как вы уже заметили, чем дальше от точки опоры мы приложим силу, тем меньшая нужна сила для совершения одной и той же работы. Причем сила нужна во столько же раз меньшая, во сколько раз больше плечо рычага. Плечо рычага – это расстояние от точки опоры или подвеса рычага до точки приложения силы (см. рис. 9).

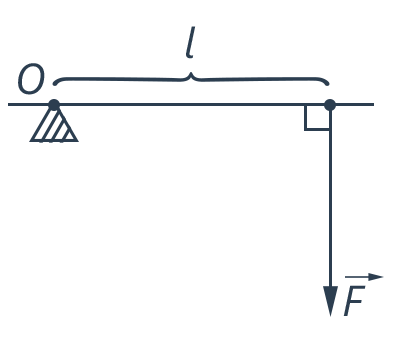
Рис. 9. Плечо рычага и сила

Силы будем прикладывать перпендикулярно рычагу.

Направление силы, действующей на рычаг

В каком направлении вы будете действовать на лопату, чтобы поднять землю? Вы приложите силу к лопате так, чтобы она оборачивалась вокруг точки опоры, то есть перпендикулярно черенку (см. рис. 10).

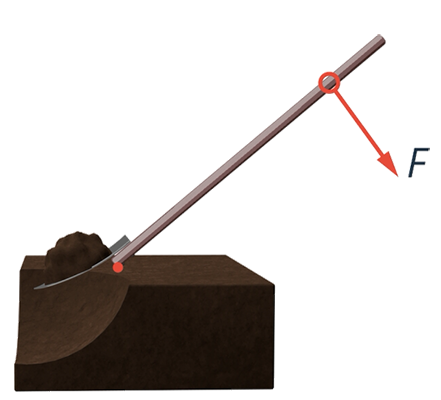
Рис. 10. Направление силы

Если вы будете действовать вдоль черенка, землю это не поднимет, вы разве что вытащите лопату из земли или воткнете ее глубже. Если вы будете давить на черенок под углом, силу можно представить как сумму двух сил: вы давите перпендикулярно черенку и одновременно толкаете или тащите вдоль черенка (см. рис. 11).

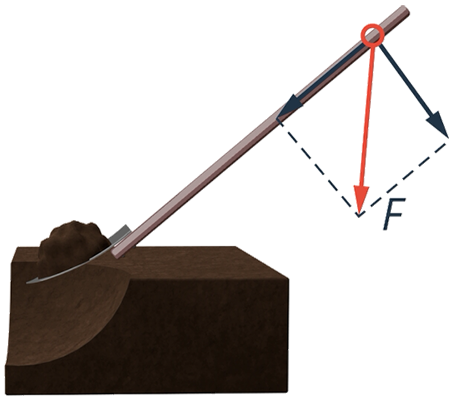
Рис. 11. Действие силы вдоль черенка

Вращать лопату будет только перпендикулярная составляющая.

Итак, у нас есть рычаг и две силы, которые на него действуют: вес груза и сила, которую мы прикладываем, чтобы этот груз поднять. Мы выявили, что чем больше плечо рычага, тем меньше нужна сила, чтобы уравновесить рычаг. Причем во сколько раз больше плечо рычага, во столько раз меньше сила. Математически это можно записать в виде пропорции:

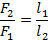
При этом неважно, приложены силы по разные стороны от точки опоры или по одну сторону. В первом случае рычаг назвали рычагом первого рода (см. рис. 12), а во втором – рычагом второго рода (см. рис. 13).

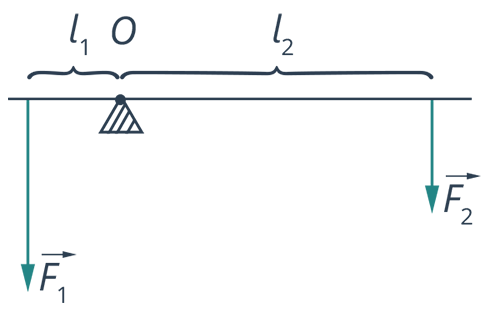
Рис. 12. Рычаг первого рода

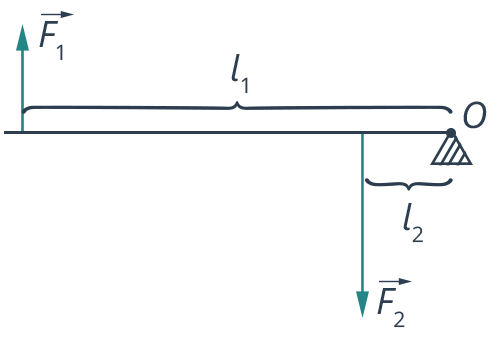
Рис. 13. Рычаг второго рода

Работа с лопатой

Мы рассмотрели, как лопата позволяет нам легче копать землю. Она опирается на край образовавшейся ямки в земле, это будет осью ее вращения. Вес земли приложен к короткому плечу рычага, мы руками прикладываем силу к длинному плечу рычага (см. рис. 14).

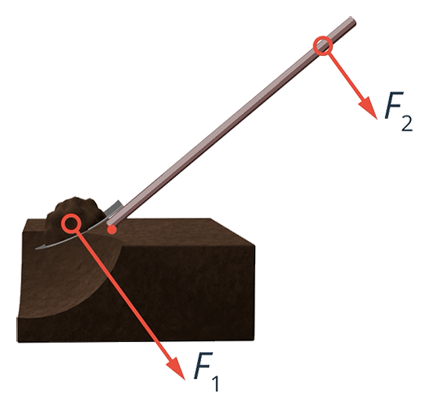
Рис. 14. Приложение сил к лопате

Причем во сколько раз отличаются плечи рычага, во столько же раз отличаются силы, приложенные к этим плечам.

Итак, мы приподняли ком земли, но дальше нужно взять лопату двумя руками, поднять ее полностью и перенести землю. Где мы возьмемся за черенок лопаты второй рукой? Всё просто, когда мы уже знаем принцип работы рычага. Вторая рука станет новой опорой рычага. Она должна быть расположена так, чтобы снова дать выигрыш в силе, она должна снова разделить рычаг на короткое и длинное плечи. Поэтому мы возьмем лопату как можно ближе к полотну лопаты. Попробуйте поднять лопату, взявшись обеими руками за край – у вас может ничего не получиться даже с пустой лопатой.

Принцип, по которому работает рычаг, используется очень часто. Например, плоскогубцы – рычаг первого рода (см. рис. 15). Мы действуем на ручки плоскогубцев с силой , а плоскогубцы действуют на кусок проволоки, трубку или гайку с силой 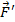, по модулю намного большей, чем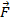

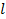. Во столько раз большей, во сколько раз

больше

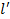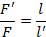
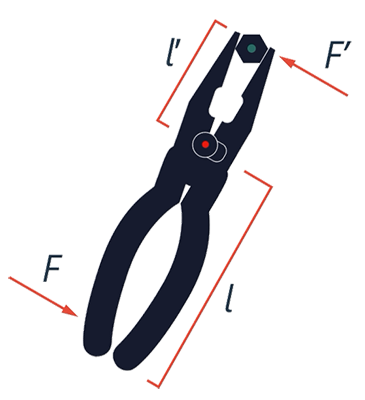
Рис. 15. Пример рычага первого рода

Еще один рычаг – консервный нож, только теперь точки приложения находятся по одну сторону от точки опоры О. И снова мы прикладываем к ручке силу , а лезвие открывалки действует на жесть консервной банки с намного большей по модулю силой (см. рис. 16).

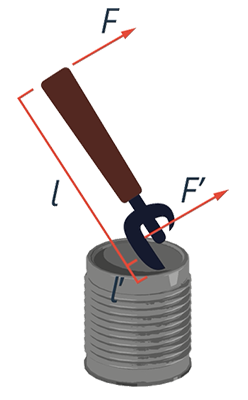
Рис. 16. Пример рычага второго рода

Во сколько раз 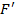больше, чем 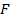? Во столько же, во сколько раз 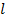больше, чем :

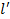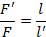
Выигрыш в силе можно получить огромный, мы ограничены разве что длиной рычага и его прочностью.

Рассчитаем, какой длины должен быть рычаг, чтобы с его помощью хрупкая девушка массой 50 кг смогла приподнять автомобиль массой 1500 кг, надавив на рычаг всем своим весом. Точку опоры рычага разместим так, чтобы короткое плечо рычага было равно 1 м (см. рис. 17).

Рис. 17. Рисунок к задаче

В задаче описан рычаг (см. рис. 18).

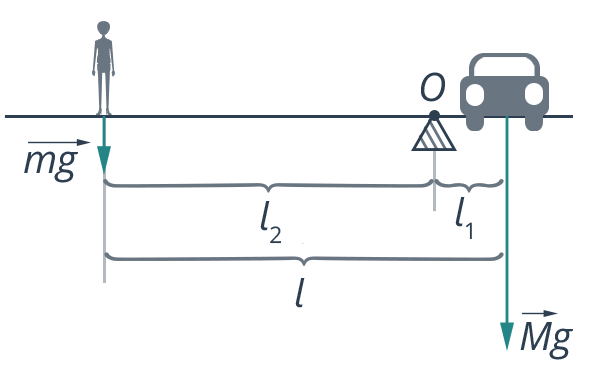
Рис. 18. Условие задачи 1

Мы знаем, во сколько раз выигрыш в силе дает рычаг:

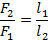
Силы прикладываются по разные стороны от опоры рычага, поэтому два плеча рычага в сумме составят его длину:

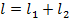
Мы описали математически процесс, заданный в условии. В нашем случае сила 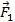, действующая на плечо 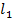, – это вес автомобиля 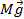, а сила 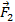, действующая на плечо 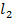, – вес девушки .

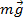Теперь осталось только решить уравнения и найти ответ.

Из первого уравнения найдем плечо 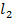.Бόльшая сила приложена к меньшему плечу рычага, значит 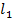– это и есть короткое плечо, равное 1 м.

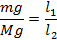
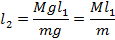
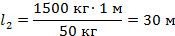
Длина рычага равна:

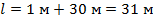
Ответ: 31 м.

Как лопата копает сама?

Рассматривая примеры, мы не учитывали силу тяжести, действующую на рычаг.

Представьте, что мы воткнули лопату неглубоко в землю. Если лопата достаточно тяжелая, небольшую массу земли она сможет поднять без нашей помощи, нам даже не нужно будет прикладывать к черенку никакую силу. Лопата повернется вокруг оси вращения под действием сил тяжести, действующей на черенок лопаты (см. рис. 19).

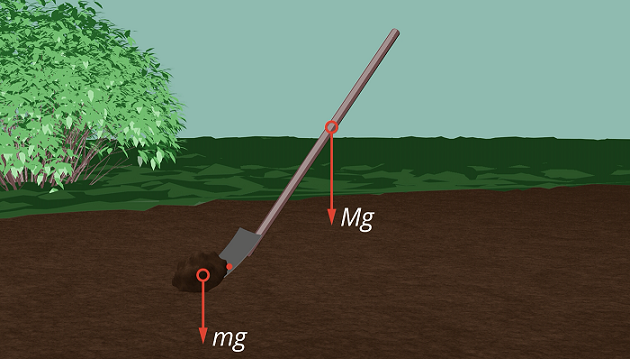
Рис. 19. Поворачивание лопаты вокруг своей оси

Однако чаще всего вес рычага пренебрежимо мал по сравнению с силами, которые на него действуют, поэтому в нашей модели мы считаем рычаг невесомым.

На примере девушки и автомобиля мы увидели, что с помощью рычага можно выполнить такую работу, которую без рычага мы бы никогда не выполнили. С помощью рычага можно было бы сдвинуть даже Землю, о чем говорил Архимед (см. рис. 20).

Рис. 20. Предположение Архимеда

Проблема в том, что рычаг не на что опереть, нет подходящей точки опоры. И вы, конечно, представляете, какой невообразимой длины должен быть такой рычаг, ведь масса Земли равна 5974 миллиарда миллиардов тонн.

Слишком всё хорошо получается: мы можем почти неограниченно уменьшать силу, необходимую для выполнения работы. Должен быть подвох, иначе с рычагом наши возможности были бы безграничны. В чем подвох?

Используя рычаг, мы прикладываем меньшую силу, но при этом совершаем большее перемещение (см. рис. 21).

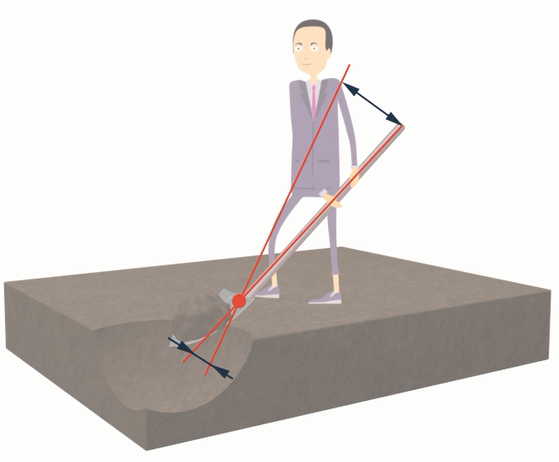
Рис. 21. Перемещение увеличивается

Мы передвинули черенок лопаты на вытянутую руку, но подняли землю всего на несколько сантиметров. Архимед, если бы всё-таки нашел точку опоры, за всю свою жизнь не успел бы повернуть свой рычаг так, чтобы сдвинуть Землю. Чем меньшую силу мы прикладываем, тем большее перемещение совершаем. А произведение силы на перемещение, то есть работа, остается постоянным. То есть рычаг дает выигрыш в силе, но проигрыш в перемещении, или наоборот.

Рычаги, которые используются «наоборот»

Не всегда рычаги используются для того, чтобы совершать работу, прикладывая меньшую силу. Иногда важно выиграть в перемещении, даже если при этом приходится прикладывать бόльшую силу. Так делает рыбак, которому нужно вытащить рыбу, переместить ее на большое расстояние. При этом он использует удочку как рычаг, прикладывая силу 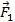к ее короткому плечу (см. рис. 22).

Рис. 22. Использование удочки

Рычагом является и наша рука. Мышцы руки сокращаются, и рука сгибается в локте. При этом она может поднять какой-нибудь груз, совершить работу. При этом на кости предплечья действуют с некоторыми силами мышцы и груз (см. рис. 23).

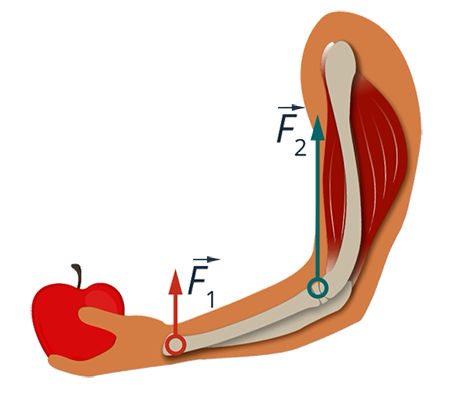
Рис. 23. Наша рука – рычаг

Ось вращения предплечья – локтевой сустав. Из таких рычагов состоит весь наш опорно-двигательный аппарат. И сам термин «плечо рычага» назван так по аналогии с плечом одного из рычагов в нашем теле – руки.

Мышцы так устроены, что они при сокращении не могут укорачиваться на те полметра, на которые нам нужно поднять, например, чашку с чаем. Нужно выиграть в перемещении, поэтому мышцы крепятся ближе к суставу, к меньшему плечу рычага. При этом нужно приложить бόльшую силу, но для мышц это не проблема.

Рычаг – не единственный простой механизм, который облегчает нам выполнение работы.

Каким простым механизмом вы пользуетесь, когда поднимаетесь на первый этаж? Можно допрыгнуть до окна, если получится, и просто вскарабкаться в комнату. Мы привыкли совершать ту же работу по перемещению себя домой намного безопаснее и легче – поднимаясь по лестнице. Так мы проделываем больший путь, но прикладываем к себе меньшую силу. Если мы сделаем длинную пологую лестницу, подниматься станет еще легче, будем идти почти как по ровной поверхности, но путь проделать придется бόльший (см. рис. 24).

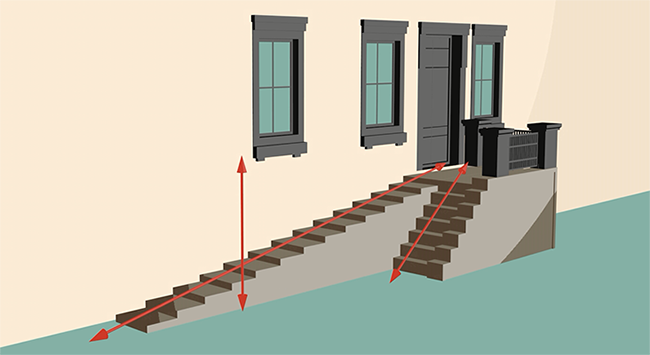
Рис. 24. Пологая лестница

Наклонная плоскость является простым механизмом. Всегда легче не поднимать что-то тяжелое, а втащить его под уклон.

Рассмотрим, как топор раскалывает древесину. Его лезвие заостренное и расширяется ближе к основанию, и чем глубже клин топора вгоняется в древесину, тем шире она раздается и в итоге раскалывается (см. рис. 25).

Рис. 25. Рубка дров

Принцип действия клина тот же, что и для наклонной плоскости. Чтобы раздвинуть части древесины на сантиметр, нужно было бы приложить огромную силу. К клину достаточно приложить меньшую силу, правда, придется совершить большее перемещение вглубь древесины.

По тому же принципу наклонной плоскости работают и винты. Присмотримся к шурупу: бороздка вдоль шурупа представляет собой наклонную плоскость, только обернутую вокруг стержня шурупа (см. рис. 26).

Рис. 26. Наклонная плоскость шурупа

И мы также без особых усилий вгоняем шуруп на нужную нам глубину. При этом, как обычно, проигрываем в перемещении: нужно сделать много оборотов шурупа, чтобы вогнать его на пару сантиметров. В любом случае это лучше, чем раздвинуть древесину и вставить туда шуруп.

Когда мы вкручиваем шуруп отверткой, мы еще больше облегчаем себе работу: отвертка представляет собой рычаг. Смотрите: сила, с которой на жало отвертки действует шуруп, приложена к меньшему плечу рычага, а мы своей рукой действуем на большее плечо (см. рис. 27).

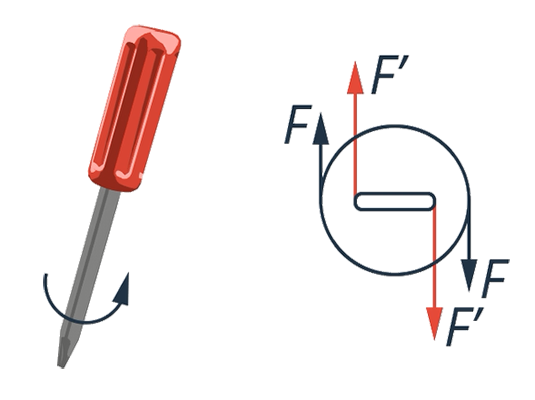
Рис. 27. Принцип работы отвертки

Рукоятка отвертки толще, чем жало. Если бы у отвертки были ручки, как у штопора, выигрыш в силе был бы еще больше.

Мы так часто пользуемся простыми механизмами, что даже не замечаем

Рычаг — Википедия

Использование рычага для получения бо́льшего усилия на коротком плече, за счёт приложения меньшей силы на длинном.

Рыча́г — твёрдое тело, которое может вращаться вокруг неподвижной опоры.

Рычаг относится к простейшим механизмам. Представляет собой любой предмет, имеющий возможность вращаться вокруг неподвижной точки опоры (подвеса). Части предмета от точки опоры до точки приложения сил называют плечами рычага. Относительно точки опоры места приложения сил могут быть по разные стороны (рычаг I рода) или с одной стороны (рычаг II рода)^[1].

Рычаг используется для создания большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие.

Частными случаями рычага являются также два других простейших механизма: дифференциальный ворот и блок.

Человек стал использовать рычаг ещё в доисторические времена, интуитивно понимая его принцип. Такие инструменты, как мотыга или весло, применялись, чтобы уменьшить силу, которую необходимо было прикладывать человеку. В пятом тысячелетии до нашей эры в Месопотамии применялись весы, использовавшие принцип рычага для достижения равновесия.^[2]^[3] Позже, в Греции, был изобретён безмен, позволивший изменять плечо приложения силы, что сделало использование весов более удобным. Около 1500 года до н. э. в Египте и Индии появляется шадуф (колодец с «журавлём»), прародитель современных кранов, устройство для поднимания сосудов с водой.^[4]

Гравюра из «Журнала механики», изданного в Лондоне в 1842 году, изображающая Архимеда, переворачивающего Землю с помощью рычага.

Неизвестно, пытались ли мыслители тех времён объяснить принцип работы рычага. Первое письменное объяснение дал в III веке до н. э. Архимед, связав понятия силы, груза и плеча. Закон равновесия, сформулированный им, используется до сих пор и звучит как: «Усилие, умноженное на плечо приложения силы, равно нагрузке, умноженной на плечо приложения нагрузки, где плечо приложения силы — это расстояние от точки приложения силы до опоры, а плечо приложения нагрузки — это расстояние от точки приложения нагрузки до опоры». По легенде, осознав значение своего открытия, Архимед воскликнул: «Дайте мне точку опоры, и я переверну Землю!»^[4].

В современном мире принцип действия рычага используется повсеместно. Практически любой механизм, преобразующий механическое движение, в том или ином виде использует рычаги. Подъёмные краны, двигатели, плоскогубцы, ножницы, а также тысячи других механизмов и инструментов используют рычаги в своей конструкции.

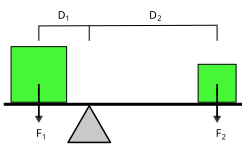Схема рычага. В равновесии F1D1=F2D2{\displaystyle F_{1}D_{1}=F_{2}D_{2}}

Принцип работы рычага является прямым следствием закона сохранения энергии. Чтобы переместить рычаг на расстояние Δh2{\displaystyle \Delta h_{1}} сила, действующая со стороны груза, должна совершить работу равную:

A1=F1Δh2{\displaystyle \ A_{1}=F_{1}\Delta h_{1}}.

Если посмотреть с другой стороны, сила, приложенная с другой стороны, должна совершать работу

A2=F2Δh3{\displaystyle \ A_{2}=F_{2}\Delta h_{2}},

где Δh3{\displaystyle \Delta h_{2}} — это перемещение конца рычага, к которому приложена сила F2{\displaystyle F_{2}}. Чтобы выполнялся закон сохранения энергии для замкнутой системы, работа действующей и противодействующей сил должны быть равны, то есть:

A1=A2{\displaystyle \ A_{1}=A_{2}},

F1Δh2=F2Δh3{\displaystyle \ F_{1}\Delta h_{1}=F_{2}\Delta h_{2}}.

По определению подобия треугольников, отношение перемещений двух концов рычага будет равно отношению его плеч:

Δh2Δh3=D1D2{\displaystyle {\frac {\Delta h_{1}}{\Delta h_{2}}}={\frac {D_{1}}{D_{2}}}}, следовательно

F1D1=F2D2{\displaystyle \ F_{1}D_{1}=F_{2}D_{2}}.

Учитывая, что произведение силы и расстояния от точки опоры до линии действия силы является модулем момента силы, можно сформулировать принцип равновесия для рычага. Рычаг находится в равновесии, если сумма моментов сил (с учётом знака), приложенных к нему, равна нулю. (Точнее, если векторная сумма моментов сил, приложенных к нему, равна нулю.)

Для рычагов, как и для других механизмов, вводят характеристику, показывающую механический эффект, который можно получить за счёт рычага. Такой характеристикой является передаточное отношение, оно показывает, как соотносятся нагрузка и приложенная сила:

i=F1F2=D2D1{\displaystyle i={\frac {F_{1}}{F_{2}}}={\frac {D_{2}}{D_{1}}}}.

Нужно отметить, что как и у любого механизма, у рычага полезная работа меньше полной. Например, у большинства рычагов коэффициент полезного действия (КПД) равен ~ 80 %. Остальные 20 процентов работы расходуются на преодоление силы трения и т. п.

В специальной теории относительности теория рычага существенно отличается от принятой в классической механике (парадокс рычага).

Составной рычаг представляет собой систему из двух и более простых рычагов, соединённых таким образом, что выходное усилие одного рычага является входным для следующего. Например, для системы из двух последовательно связанных рычагов, если на входное плечо первого рычага приложена сила F1{\displaystyle F_{1}}, на другом конце этого рычага выходное усилие окажется F2{\displaystyle F_{2}}, и связаны они будут с помощью передаточного отношения:

i1=F1F2{\displaystyle i_{1}={\frac {F_{1}}{F_{2}}}}.

При этом на входное плечо второго рычага будет воздействовать такое же усилие F2{\displaystyle F_{2}}, а выходным усилием второго рычага и всей системы будет F3{\displaystyle F_{3}}, передаточное отношение второй ступени будет равно:

i2=F2F3{\displaystyle i_{2}={\frac {F_{2}}{F_{3}}}}.

При этом механический эффект всей системы, то есть всего составного рычага, будет вычисляться как отношение входного и выходного усилия для всей системы, то есть:

i=F1F3=F1F3F2F2=F1F2F2F3=i1i2{\displaystyle i={\frac {F_{1}}{F_{3}}}={\frac {F_{1}}{F_{3}}}{\frac {F_{2}}{F_{2}}}={\frac {F_{1}}{F_{2}}}{\frac {F_{2}}{F_{3}}}=i_{1}i_{2}}.

Таким образом, передаточное отношение составного рычага, состоящего из двух простых будет равно произведению передаточных отношений входящих в него простых рычагов.

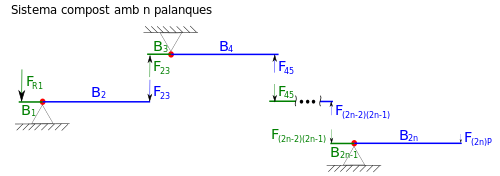$i={\frac {F_{1}}{F_{3}}}={\frac {F_{1}}{F_{3}}}{\frac {F_{2}}{F_{2}}}={\frac {F_{1}}{F_{2}}}{\frac {F_{2}}{F_{3}}}=i_{1}i_{2}$

Составной рычаг в общем случае, состоящий из n простых рычагов

Такой же подход решения можно применять и для более сложной системы, состоящей, в общем случае из n рычагов. В этом случае в системе будет присутствовать 2n плеч. Передаточное отношение для такой системы будет вычисляться по формуле:

iC=FR1F(2n−1)−P=FR1F23⋅F23F45⋅…⋅F(2n−2)−(2n−1)F(2n−1)−P=B2B1⋅B4B3⋅…⋅B(2n)B(2n−1){\displaystyle i_{C}={\frac {F_{R1}}{F_{(2n-1)-P}}}={\frac {F_{R1}}{F_{23}}}\cdot {\frac {F_{23}}{F_{45}}}\cdot …\cdot {\frac {F_{(2n-2)-(2n-1)}}{F_{(2n-1)-P}}}={\frac {B_{2}}{B_{1}}}\cdot {\frac {B_{4}}{B_{3}}}\cdot …\cdot {\frac {B_{(2n)}}{B_{(2n-1)}}}},

где:

Bi{\displaystyle \ B_{i}} — это i-ое плечо системы;
F(i−1)i{\displaystyle \ F_{(i-1)i}} — сила, передаваемая с плеча (i-1) на плечо i;
iC{\displaystyle \ i_{C}} — передаточное отношение всей системы.

Как видно из формулы для этого случая также верно, что передаточное отношение составного рычага равно произведению передаточных отношений входящих в него элементов.

Различают рычаги 1 рода, в которых точка опоры располагается между точками приложения сил, и рычаги 2 рода, в которых точки приложения сил располагаются по одну сторону от опоры. Среди рычагов 2 рода выделяют рычаги 3 рода^[5], с точкой приложения внешней силы ближе к точке опоры, чем нагрузки, что даёт выигрыш в скорости и пути.

Примеры: рычаги первого рода — детские качели (перекладина), ножницы; рычаги второго рода — тачка (точка опоры — колесо), приподнимание предмета ломом движением вверх; рычаги третьего рода — метла дворника, грабли; задняя дверь багажника или капот легковых автомобилей на гидравлических телескопических упорах, подъём кузова самосвала (с гидроцилиндром в центре), движение мышцами рук и ног человека и животных.

Простые механизмы. Рычаг (рычаг первого рода и рычаг второго рода). Блок (неподвижный блок и подвижный блок). Наклонная плоскость. Гидравлический пресс. Золотое правило механики

Рычаг (рычаг первого рода и рычаг второго рода):
Рычаг первого рода: ось вращения расположена между точками приложения сил, а сами силы направлены в одну сторону. Рычаг второго рода: ось вращения расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу. Система отсчета: совокупность тела отсчета (относительно которого рассматривается движение), связанных с ним системы координат и способа измерения времени.
Блок:
Неподвижный блок (равноплечный рычаг первого рода): выйгрыша в силе не дает. *F=mg* — он позволяет менять направление и только Подвижный блок (рычаг второго рода) дает выйгрыш в силе в 2 раза:
Наклонная плоскость:
Для равномерного подъёма груза с помощью наклонной плоскости необходимо приложить силу, во столько раз меньшую силы тяжести груза, во сколько раз длина наклонной плоскости больше её высоты:
Гидравлический пресс:
Гидравлический пресс дает выйгрыш в силе во столько раз, во сколько площадь большого поршня боль

Рычаг | Физика

Сила человека ограничена. Поэтому он часто применяет устройства (или приспособления), позволяющие преобразовать его силу в силу, существенно большую. Примером подобного приспособления является рычаг.

Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры. В качестве рычага могут быть использованы лом, доска и тому подобные предметы.

Различают два вида рычагов. У рычага 1-го рода неподвижная точка опоры O располагается между линиями действия приложенных сил (рис. 47), а у рычага 2-го рода она располагается по одну сторону от них (рис. 48).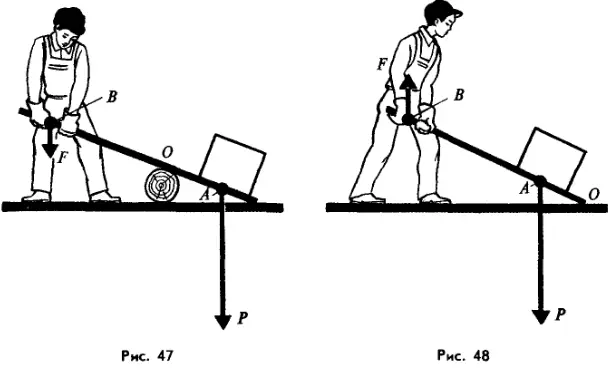Использование рычага позволяет получить выигрыш в силе. Так, например, рабочий, изображенный на рисунке 47, прикладывая к рычагу силу 400 Н, сможет приподнять груз весом 800 Н. Разделив 800 Н на 400 Н, мы получим выигрыш в силе, равный 2.

Для расчета выигрыша в силе, получаемого с помощью рычага, следует знать правило, открытое Архимедом еще в III в. до н. э. Для установления этого правила проделаем опыт. Укрепим на штативе рычаг и по обе стороны от оси вращения прикрепим к нему грузы (рис. 49). Действующие на рычаг силы F₁ и F₂ будут равны весам этих грузов. Из опыта, изображенного на рисунке 49, видно, что если плечо одной силы (т. е. расстояние OA) в 2 раза превышает плечо другой силы (расстояние OB), то силой 2 Н можно уравновесить в 2 раза большую силу – 4 Н.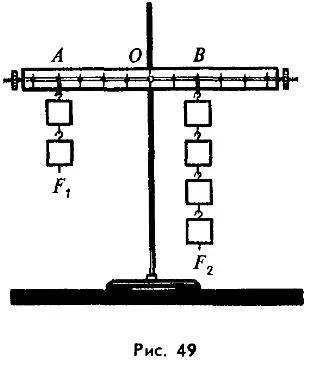Итак, для того чтобы уравновесить меньшей силой большую силу, необходимо, чтобы ее плечо превышало плечо большей силы. Выигрыш в силе, получаемый с помощью рычага, определяется отношением плеч приложенных сил. В этом состоит правило рычага.

Обозначим плечи сил через l₁ и l₂ (рис. 50). Тогда правило рычага можно представить в виде следующей формулы:

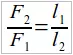(20.1)

Эта формула показывает, что рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам.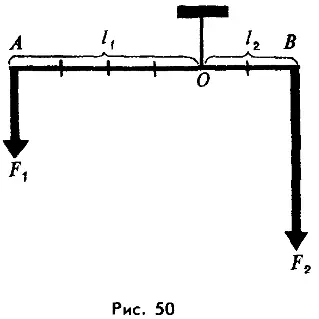

Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте (рис. 51). Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту 147 м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу 2,5 т!

В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы и т. д.).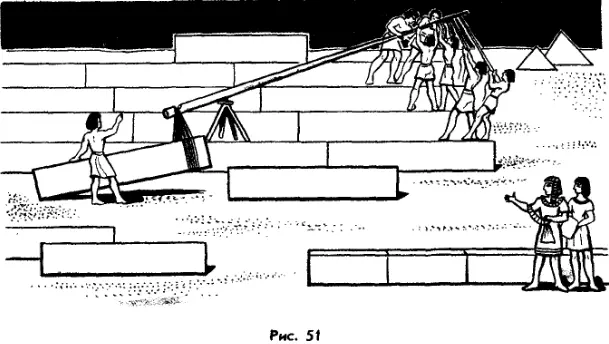

1. Что представляет собой рычаг? 2. В чем заключается правило рычага? Кто его открыл? 3. Чем отличается рычаг 1-го рода от рычага 2-го рода? 4. Приведите примеры применения рычагов. 5. Рассмотрите рисунки 52, а и 52, б. В каком случае груз нести легче? Почему?
Экспериментальное задание. Положите под середину линейки карандаш так, чтобы линейка находилась в равновесии. Не меняя взаимного расположения линейки и карандаша, уравновесьте иа полученном рычаге одну монету с одной стороны и стопку из трех таких же монет с другой стороны. Измерьте плечи приложенных (со стороны монет) сил и проверьте правило рычага.

Что это рычаг в физике? Принцип работы рычага. Виды рычагов

Каждый современный человек, который слышит слово «механизм», представляет себе набор шурупов, гаек, металлических прутьев, пружин, поршней, дисков и валов. В действительности же под этим словом обычно понимали более простые вещи, например, деревянный клин или обычную наклонную плоскость. Упомянутые механизмы называются простыми. Одним из них является рычаг. Рассмотрим в статье, что это — рычаг.

Физическое понятие о рычаге

Рычаг — это простой механизм, служащий для облегчения выполнения многих видов работ, например, подъем тяжестей или сообщение телам начальной скорости. Рычаг состоит из двух элементов: балки определенной длины и одной опоры. Опора, располагаемая под балкой, делит рычаг на два плеча. Соотношение их длин является принципиальным во время применения этого механизма.

На рисунке выше показан рассмотренный простой механизм, который является рычагом первого рода (см. ниже).

Историческая справка

Каждый школьник слышал уже в 7 классе о знаменитом рычаге Архимеда. Греческий философ утверждал, что при определенных размерах этого простого механизма он мог бы перевернуть нашу Землю, будь вторая такая планета, которую можно было бы использовать в качестве опоры. Архимеду действительно принадлежит большая заслуга в развитии статики, поскольку он смог экспериментально получить математическое равенство, которое в настоящее время носит название «Условия равновесия рычага».

Однако сам принцип рычага использовался задолго до нашей эры. Так, известно, что для забора воды из рек применялся этот простой механизм. Существуют исторические свидетельства, что при строительстве пирамид египтяне также применяли систему рычагов.

Принцип работы рычага

Познакомившись с вопросом, что такое рычаг в физике (это наипростейший механизм), перейдем к рассмотрению принципа, согласно которому с помощью рычага получается выигрыш в силе или в пути перемещения. Для этого вспомним, что в физике существует величина, которая называется моментом силы. Последний равен произведению плеча силы на модуль силы, то есть:

M = d*F.

Где плечо силы d — это дистанция от опоры рычага до точки действия силы F.

Если вспомнить статику, то второе условие равновесия системы твердых тел в ней гласит, что система не будет совершать вращательного движения, если сумма всех n моментов сил в ней равна нулевому значению. То есть:

∑_i=1ⁿM_i= 0.

Прежде чем переходить к формулировке условия равновесия рычага, отметим, что момент силы, который стремится повернуть систему против часовой стрелки, является положительным. Противоположный ему момент будет отрицательным.

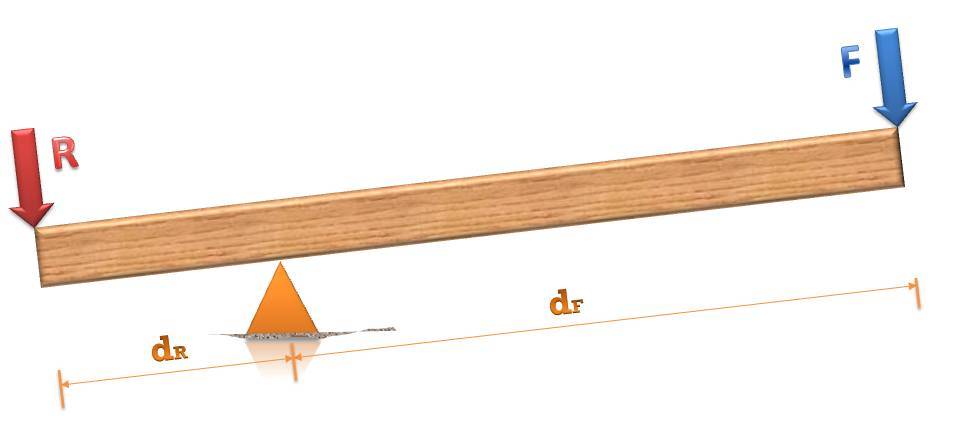
Выше показан рычаг, на который оказывают действие внешняя сила F и сила нагрузки R. Учитывая значение плеч сил и направления моментов, можно записать следующее равенство:

R*d_R — F*d_F = 0.

Откуда получаем условие равновесия рычага, полученное еще Архимедом:

d_R/d_F = F/R.

Это условие говорит о том, что чем длиннее плечо d_F, тем меньшую силу F следует приложить, чтобы поднять вес R. При этом высота подъема этого веса будет меньше, чем высота, на которую опустится плечо d_F. Таким образом, при d_F>d_R получается выигрыш в силе, но проигрыш в пути. При обратном соотношении плеч получится выигрыш уже в пути, но силу F придется приложить большей величины, чем вес R.

Таким образом рычаг можно применять как для подъема тяжестей, так и для сообщения скорости телу весом R. Последнее раньше использовалось в катапультах.

Виды рычагов и примеры

В зависимости от положения опоры и порядка расположения действующих на балку сил рычаги бывают трех родов. Расскажем кратко об особенностях каждого из них.

Рычаг — это устройство, которое может быть нескольких видов. Первого рода рычаги являются двуплечими. В соответствии с соотношением длин плеч он может давать выигрыш в силе или в пути. Примерами применения таких рычагов являются ножницы, детские качели, гвоздодер.

Рычаг — это механизм не только двуплечий. Он также может иметь одно плечо, когда опора располагается вблизи края балки. В этом случае возможно два варианта в расположении точек приложения сил F и R, которые были рассмотрены ранее. Если F лежит дальше от опоры, чем R, то мы получаем рычаг второго рода, если же F ближе к опоре, чем R, то получаем рычаг третьего рода. Рычагами второго рода являются ручная тачка для перемещения грузов или орехокол.

В качестве рычагов третьего рода можно привести в пример рыбацкую удочку, пинцет или столовую вилку.

Нетрудно понять, что рычаги второго рода дают выигрыш в силе, а третьего рода — в пути.

Виды рычагов в физике

Равновесие в физике представляет собой состояние системы, при котором она находится в относительном покое к окружающим объектам. Изучением условий равновесия занимается статика. Одним из механизмов, знание условий равновесия для работы которого имеет принципиальное значение, является рычаг. Рассмотрим в статье, какие виды рычагов бывают.

Что это в физике?

Прежде чем говорить о видах рычагов (в физике 7 класса проходят данную тему), дадим определение этому устройству. Рычаг — это простой механизм, который позволяет преобразовывать силу в расстояние и наоборот. Рычаг имеет простое устройство, он состоит из балки (доски, стержня), которая имеет определенную длину, и из одной опоры. Положение опоры не является фиксированным, поэтому она может располагаться как на середине балки, так и на ее конце. Сразу отметим, что положение опоры в общем определяет вид рычага.

Последний используется человеком с незапамятных времен. Так, известно, что в древней Месопотамии или в Египте с помощью него поднимали из рек воду или перемещали огромные камни при строительстве различных сооружений. Активно использовали рычаг в Античной Греции. Единственное письменное свидетельство, которое сохранилось об использовании этого простого механизма — это «Параллельные жизни» Плутарха, где философ приводит пример использования системы блоков и рычагов Архимедом.

Понятие о вращающем моменте

Понимание принципа работы разного вида рычагов в физике возможно, если изучить вопрос равновесия рассматриваемого механизма, которое тесным образом связано с понятием момента силы.

Момент силы — это величина, которая получается, если умножить силу на расстояние от точки ее приложения до оси вращения. Это расстояние принято называть «плечом силы». Обозначим F и d — силу и ее плечо соответственно, тогда получаем:

M = F*d

Момент силы обеспечивает возможность совершить поворот вокруг данной оси всей системы. Яркими примерами, в которых можно наблюдать момент силы в действии, являются откручивание гаечным ключом гайки или открывание двери за ручку, находящуюся далеко от дверных петель.

Вращающий момент является векторной величиной. В решении задач часто приходится учитывать его знак. Следует запомнить, что всякая сила, вызывающая вращение системы тел против часовой стрелки, создает момент силы со знаком +.

Равновесие рычага

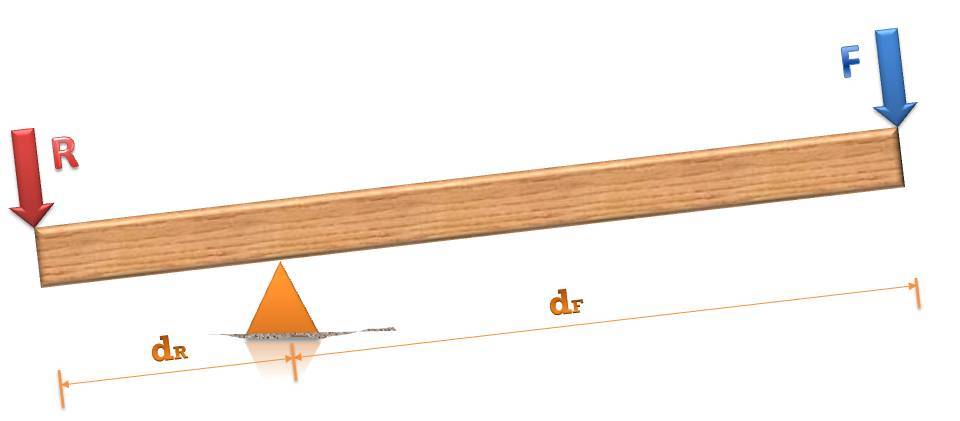
На рисунке выше показан типичный рычаг и отмечены силы, которые на него действуют. Далее в статье будет сказано, что это — рычаг первого рода. Здесь буквами F и R отмечены внешняя сила и некоторый вес груза соответственно. Также видно, что опора смещена относительно центра, поэтому длины плеч d_F и d_R не равны друг другу.

В статике показано, чтобы рычаг не двигался как целый механизм, должна нулю равняться сумма всех сил, которые на него действуют. Мы отметили только две из них. На самом деле существует еще и третья, которая этим двум противоположна и равна их сумме — это реакция опоры.

Чтобы рычаг не совершал вращательные движения, необходимо, чтобы сумма всех моментов сил была равна нулю. Плечо силы реакции опоры равно нулю, поэтому момента она не создает. Остается записать моменты сил F и R:

R*d_R — F*d_F = 0 =>
R*d_R = F*d_F

Записанное условие равновесия рычага в виде формулы, также приводится:

d_R/d_F = F/R

Это равенство означает, что для того, чтобы рычаг не совершал вращение, внешняя сила должна быть во столько раз больше (меньше) веса поднимаемого груза, во сколько раз плечо этой силы меньше (больше) плеча, на которое действует вес груза.

Приведенная формулировка означает, что во сколько раз мы выигрываем в пути с помощью рассматриваемого механизма, во столько же раз проигрываем в силе.

Рычаг первого рода

Он был показан в предыдущем пункте. Здесь лишь скажем, что для рычага данного вида опора расположена между действующими силами F и R. В зависимости от соотношения длин плеч такой рычаг может применяться как для подъема тяжестей, так и для придания телу ускорения.

Примерами рычагов первого рода являются механические весы, ножницы, гвоздодер, катапульта.

В случае весов мы имеет два плеча одинаковой длины, поэтому равновесие рычага достигается только в том случае, когда силы F и R равны друг другу. Этот факт используется для взвешивания тел неизвестной массы путем сравнения ее с эталонным значением.

Ножницы и гвоздодер — это яркие примеры выигрыша в силе, но проигрыша в пути. Каждый знает, что чем ближе к оси ножниц заложен лист бумаги, тем легче ее отрезать. Наоборот, если попытаться отрезать кончиками ножниц бумагу, то высока вероятность, что они начнут ее «жевать». Чем длиннее ручка ножниц или гвоздодер, тем легче выполнить с помощью них соответствующие операции.

Что касается катапульты, то это яркий пример выигрыша с помощью рычага в пути, а значит, и в ускорении, которое его плечо сообщает снаряду.

Рычаг второго рода

Во всех рычагах второго рода опора находится вблизи одного из концов балки. Это ее расположение приводит к наличию всего одного плеча у рычага. При этом вес груза расположен всегда между опорой и внешней силой F. Расположение сил в рычаге второго рода приводит к единственному полезному результату: выигрышу в силе.

Примерами этого вида рычага являются тачка ручная, которая служит для перевозки тяжелых грузов, а также орехокол. В обоих случаях проигрыш в пути не имеет никакого отрицательного значения. Так, в случае ручной тачки важно лишь удерживать груз на весу во время его перемещения. При этом прилагаемая сила оказывается в несколько раз меньше веса груза.

Рычаг третьего рода

Конструкция рычага этого вида во многом подобна предыдущему. Опора в этом случае также расположена на одном из концов балки, и рычаг обладает единственным плечом. Однако расположение действующих сил в нем совершенно иное, чем в рычаге второго рода. Точка приложения силы F находится между весом груза и опорой.

Яркими примерами этого вида рычага являются лопата, шлагбаум, удочка и пинцет. Во всех этих случаях мы в пути выигрываем, однако происходит существенный проигрыш в силе. Например, чтобы удержать тяжелый груз с помощью пинцета, необходимо приложить большую силу F, поэтому использование этого инструмента не подразумевает удержание с помощью него тяжелых предметов.

В заключение отметим, что все виды рычагов работают по одному и тому же принципу. Они не дают выигрыша в работе по перемещению грузов, а лишь позволяют перераспределить эту работу в сторону более удобного ее выполнения.

Простые механизмы. Рычаг. Равновесие сил на рычаге

Цели урока

Образовательная:

ввести понятие «простой механизм»;
изучить устройство и принцип действия рычага;
выяснить условие равновесия рычага;
исследовать использование простых механизмов в природе и технике.

Развивающие:

способствовать развитию умения анализировать, выдвигать гипотезы, предположения, строить прогнозы, наблюдать и экспериментировать;
способствовать развитию логического мышления;
развитие учебно-коммуникативных умений (задавать вопросы, объяснять и доказывать свою точку зрения).

Воспитательные:

способствование расширению политехнического кругозора учащихся;
пробуждение познавательного интереса к предмету и окружающим явлениям.

Планируемые результаты

Ученики приобретут знания о

простых механизмах;
видах простых механизмов;
плече силы;
условии равновесия рычага;
практическом применении рычага.

Ученики приобретут умения:

измерять плечо силы;
экспериментально определять соотношение сил и плеч для равновесия рычага.

Ученики закрепят навыки и умения:

планировать эксперимент;
выбирать главное из текста;
анализировать информацию;
делать выводы.

Тип урока: урок открытия нового знания

Вид урока: урок – исследование

Оборудование: штатив, набор грузов, рычаги, динамометр, ножницы, гаечный ключ, щипцы.

План урока

Организационный момент (1 мин)
Мотивационный момент (3 мин)
Освоение нового материала (20 мин)
Первичная проверка усвоения знаний (10 мин)
Первичное закрепление знаний (7 мин)
Подведение итогов урока (рефлексия) (3 мин)
Домашнее задание (1 мин)

Ход урока

1. Организационный момент. Психологический настрой

2. Мотивация учащихся.

Учитель: Здравствуйте, ребята. Сегодня у нас необычный урок: урок-исследование.

Для начала решим задачу:

Штангист держит штангу весом 2 кН на высоте 2,5 м. Какую работу при этом он совершает? (А = mgh = 2ּ 10³Н ּ 2,5м = 5ּ 10³ = 5кДж).

А, если это будет более тяжелый предмет, например, шкаф. Как его приподнять? Зачастую человеческой силы для этого недостаточно. Что делать? Ученики: Можно подсунуть под край шкафа крепкую палку или, например, клюшку.

Учитель: Верно. А, чтобы разрезать ткань, например, используют ножницы. Чтобы открутить гайку используют гаечный ключ.

Все эти приспособления с точки зрения физики называются одинаково – рычаг. Как вы думаете, для чего нужен рычаг?

Ученики: Для того чтобы увеличить силу, прикладываемую человеком.

3. Освоение нового материала

Учитель: Приспособления, служащие для преобразования силы, называют механизмами. Рычаг – один из первых простейших механизмов, изобретенных человеком. Рычаг – это любое твердое тело, способное вращаться вокруг какой — либо неподвижной опоры. (Учащиеся записывают тему урока и определение рычага).

Чтобы поднять тяжелый груз на некоторую высоту, его вкатывают по наклонной плоскости или поднимают с помощью блоков. Таким образом, наклонная плоскость и блок – это тоже простые механизмы. Приведите примеры простых механизмов, которые вам встречались в быту, технике.

Ученики: качели, весло, щипцы, плоскогубцы, весы, подъемный кран.

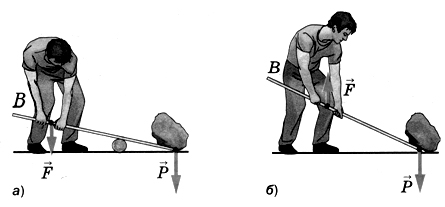
Учитель: Различают два вида рычагов:

У рычага 1 рода (рис. а) точка опоры располагается между линиями действия приложенных сил, а у рычага 2 рода (рис. б) она располагается по одну сторону от них.

Создание проблемной ситуации

Учитель: Почему качели находятся в равновесии?

Ученики выдвигают гипотезы: Кот и ежик сидят на разных расстояниях от оси вращения (точки опоры) и имеют разный вес.

Учитель: Меньшей силой уравновешена большая сила. Какой можно сделать вывод?

Ученики: Чтобы меньшей силой уравновесить большую, нужно увеличить расстояние от точки опоры до линии действия меньшей силы.

Учитель: Будут ли в равновесии эти рычаги? Как уравновесить эти рычаги?

Учитель: У вас на столах рычаг на штативе, грузы и динамометр. На левую часть рычага подвесьте два груза. Опытным путем установите, на каком расстоянии вправо от оси вращения надо подвесить: а) один груз: б) два груза; в) три груза, чтобы рычаг пришел в равновесие.

Сделайте вывод о соотношении сил и расстояний от точки опоры до линии действия сил.

Ученики: Если силы (вес грузов) отличаются в 2 раза, то и расстояния, на которых подвешены грузы также отличаются в 2 раза. Причем большая сила должна быть приложена на меньшем расстоянии от точки опоры.

Учитель: Кратчайшее расстояние от линии действия силы до точки опоры называется плечом силы. Найдите в учебнике правило нахождения плеча силы. (Работают с учебником).

Учащиеся записывают определение плеча силы.

Ученик зачитывает: Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.

Учитель: Рычаг позволяет получить выигрыш в силе — это отношение сил F1/ F2.

Условие равновесия рычага:

Вывод: рычаг находится в равновесии, если отношение сил обратно пропорционально отношению расстояний.

Учащиеся записывают в тетрадь условие равновесия рычага.

4. Первичная проверка усвоения знаний

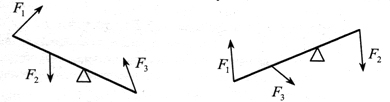
Учитель предлагает указать на рисунках плечи сил:

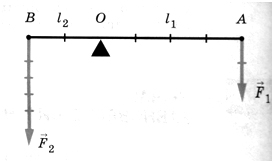
Учитель предлагает решить расчетную задачу: Длина одного плеча рычага 12 см, другого – 24 см. На меньшем плече подвешен груз массой 50 кг. Какая сила должна действовать на другое плечо рычага, чтобы он находился в равновесии?

Учитель предлагает проделать экспериментальное задание: Возьмите спичку и разломите ее пополам, получившиеся части снова разломите пополам, и так продолжайте ломать спичку на все более маленькие кусочки. Почему маленькие кусочки труднее разламывать, чем большие?

Учащиеся проделывают задание и отвечают на вопрос.

Физминутка: Встаньте, сначала повращайте одной рукой, затем — другой. Теперь приподнимитесь на носочках. Вы знаете, стопы ног, руки – это тоже рычаги.

5. Первичное закрепление знаний

Класс делится на 3 группы, каждая группа получает задание:

Задание 1 группе

Оборудование: ножницы разных видов, кусачки, гаечный ключ, линейка.

Измерьте с помощью линейки плечи рычагов. Определите выигрыш в силе данных простых механизмов.

Задание 2 группе

Сконструировать из подручного материала один из простых механизмов и продемонстрировать его в действии.

Задание 3 группе

Составить ребусы, кроссворд на тему: Простые механизмы в природе.

6. Подведение итогов урока (рефлексия)

Что называется простыми механизмами?
Какие виды простых механизмов вы знаете?
Что такое рычаг?
Что называется плечом силы?
Каково правило равновесия рычага?
Где применяется в нашей жизни рычаг?
Какое значение имеют простые механизмы в жизни человека?

Учащиеся отвечают на вопросы.

7. Домашнее задание

§ 57, 58, 60; задачи № 736, 742, 747.

Домашние опыты:

Положите под середину линейки карандаш так, чтобы линейка находилась в равновесии. Не изменяя взаимного расположения линейки и карандаша, уравновесьте на полученном рычаге одну монету с одной стороны и стопку из трех таких же монет с другой стороны. Измерьте плечи приложенных (со стороны монет) сил и проверьте правило рычага.
Определите массу линейки. У вас имеются измерительная линейка, карандаш и монета. Масса монеты считать известной, равной m.

Учитель: Желаю Вам найти свою точку опоры и всегда оставаться в равновесии! Спасибо за урок!